
 如图,在平面直角坐标系中,A(2,2),B(-1,0),C (3,0)
如图,在平面直角坐标系中,A(2,2),B(-1,0),C (3,0)分析 (1)根据点B、C的坐标即可得出线段BC的长度,再结合点A的纵坐标利用三角形的面积公式即可求出△ABC面积;
(2)设点D的坐标为(x,0),由三角形的面积公式结合△AOD的面积是△ABC面积的2倍,即可得出关于x的一元一次方程,解之即可得出结论;
(3)假设存在,过点P作PE⊥AO于点E,延长OA交直线x=3于点F,由点O、A的坐标利用待定系数法求出直线OA的解析式,进而即可求出点F的坐标,由点F的坐标结合PE⊥AO即可找出△PEF为等腰直角三角形,由此可得出PE=$\frac{\sqrt{2}}{2}$PF,再根据△AOP的面积等于△ABC面积的2倍即可得出关于m的含绝对值符号的一元一次方程,解之即可得出m值.
解答 解:(1)∵点B(-1,0),C(3,0),
∴BC=3-(-1)=4.
∴S△ABC=$\frac{1}{2}$BC•yA=$\frac{1}{2}$×4×2=4.
(2)设点D的坐标为(x,0),
∵△AOD的面积是△ABC面积的2倍,
∴S△AOD=$\frac{1}{2}$OD•yA=|x|=2S△ABC=8,
∴x=±8.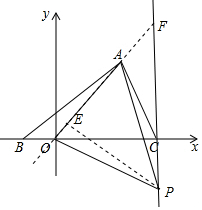
∴点D的坐标为(-8,0)和(8,0).
(3)假设存在,过点P作PE⊥AO于点E,延长OA交直线x=3于点F,如图所示.
由点O(0,0)、A(2,2)利用待定系数法可得出直线OA的解析式为y=x,
联立直线OA和CP成方程组,
$\left\{\begin{array}{l}{y=x}\\{x=3}\end{array}\right.$,解得:$\left\{\begin{array}{l}{x=3}\\{y=3}\end{array}\right.$,
∴点F(3,3),
∴OC=CF=3,
∴∠OFC=45°.
∵PE⊥OA,
∴△PEF为等腰直角三角形,
∴PE=$\frac{\sqrt{2}}{2}$PF.
∵点O(0,0),点A(2,2),
∴OA=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$.
∵S△AOP=$\frac{1}{2}$OA•PE=$\frac{1}{2}$×2$\sqrt{2}$×$\frac{\sqrt{2}}{2}$|3-m|=2S△ABC=8,
∴|3-m|=8,
解得:m=-5或m=11.
故存在m值,使△AOP的面积等于△ABC面积的2倍,此时m的值为-5或11.
点评 本题考查了坐标与图形的性质、待定系数法求一次函数解析式、等腰直角三角形的判定与性质、三角形的面积以及解一元一次方程,解题的关键是:(1)熟练掌握三角形的面积公式;(2)根据面积间的关系找出关于x的一元一次方程;(3)根据面积间的关系找出关于m的一元一次方程.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
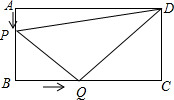 如图所示,在长方形ABCD中,AB=6厘米,BC=12厘米,点P沿AB边从点A开始向点B以1厘米/秒的速度移动,点Q沿BC从点B开始向点C以2厘米/秒的速度移动,如果P、Q同时出发,用t(秒)表示移动的时间(0≤t≤6).
如图所示,在长方形ABCD中,AB=6厘米,BC=12厘米,点P沿AB边从点A开始向点B以1厘米/秒的速度移动,点Q沿BC从点B开始向点C以2厘米/秒的速度移动,如果P、Q同时出发,用t(秒)表示移动的时间(0≤t≤6).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 工作时间t(小时) | 1 | 5 | 10 | 15 | 20 | … | t | … |
| 报酬m(元) | 20 | 100 | 200 | 300 | 400 | … | 20t | … |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
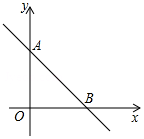 如图,直线y=$\frac{\sqrt{3}}{3}x$+1和x轴、y轴分别交于点A、B.若以线段AB为边作等边三角形ABC,则点C的坐标是($\sqrt{3}$,2)或(0,-1).
如图,直线y=$\frac{\sqrt{3}}{3}x$+1和x轴、y轴分别交于点A、B.若以线段AB为边作等边三角形ABC,则点C的坐标是($\sqrt{3}$,2)或(0,-1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC中,∠BAC=45°,过A、B两点的⊙O交AC于点D,且OD∥BC,OD交AB于点E.
如图,△ABC中,∠BAC=45°,过A、B两点的⊙O交AC于点D,且OD∥BC,OD交AB于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
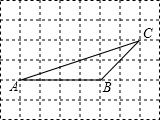 如图,在方格纸中,点A、B、C是三个格点(网格线的交点叫做格点)
如图,在方格纸中,点A、B、C是三个格点(网格线的交点叫做格点)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
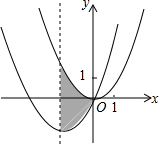 如图,抛物线C1:y=$\frac{1}{2}$x2经过平移得到抛物线C2:y=$\frac{1}{2}$x2+2x,抛物线C2的对称轴与两段抛物线所围成的阴影部分的面积是4.
如图,抛物线C1:y=$\frac{1}{2}$x2经过平移得到抛物线C2:y=$\frac{1}{2}$x2+2x,抛物线C2的对称轴与两段抛物线所围成的阴影部分的面积是4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com