练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，直线a∥b，∠1︰∠2︰∠3 =2︰3︰6 ，求∠1的度数．

    40°．

    解析试题分析：由∠1︰∠2︰∠3 =2︰3︰6，可设∠1、∠2、∠3的度数分别为2x°、 3x°、6x°，根据平行线同旁内角互补的性质得3x+6x=180，求解x即能求得∠1．
    ∵∠1︰∠2︰∠3 =2︰3︰6，
    ∴可设∠1、∠2、∠3的度数分别为2x°、 3x°、6x°．
    ∵a∥b，
    ∴∠2+∠3=180°．
    ∴3x+6x=180，解得： x=20．
    ∴∠1=2x°=2×20°=40°．
    考点：平行线的性质．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    将一个长方形纸条按图所示折叠一下，若∠1=140º，则∠2=______.

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    问题情境：将一副直角三角板（Rt△ABC和Rt△DEF）按图1所示的方式摆放，其中∠ACB=90°，CA=CB，∠FDE=90°，O是AB的中点，点D与点O重合，DF⊥AC于点M，DE⊥BC于点N，试判断线段OM与ON的数量关系，并说明理由．
    探究展示：小宇同学展示出如下正确的解法：
    解：OM=ON，证明如下：
    连接CO，则CO是AB边上中线，
    ∵CA=CB，∴CO是∠ACB的角平分线．（依据1）
    ∵OM⊥AC，ON⊥BC，∴OM=ON．（依据2）
    反思交流：
    （1）上述证明过程中的“依据1”和“依据2”分别是指：
    依据1：                                                        ；
    依据2：                                                        ．
    （2）你有与小宇不同的思考方法吗？请写出你的证明过程．
    拓展延伸：
    （3）将图1中的Rt△DEF沿着射线BA的方向平移至如图2所示的位置，使点D落在BA的延长线上，FD的延长线与CA的延长线垂直相交于点M，BC的延长线与DE垂直相交于点N，连接OM、ON，试判断线段OM、ON的数量关系与位置关系，并写出证明过程．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图，已知四边形ABCD，AD∥BC．点P在直线CD上运动（点P和点C，D不重合，点P，A，B不在同一条直线上），若记∠DAP，∠APB，∠PBC分别为．
    （1）当点P在线段CD上运动时，写出之间的关系并说出理由；
    （2）如果点P在线段CD（或DC）的延长线上运动，探究之间的关系，并选择其中的一种情况说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    已知：如图，直线AB与直线BC相交于点B，点D是直线BC上一点，求作：点E，使直线DE∥AB，且点E到B、D两点的距离相等．（尺规作图，要求在题目的原图中完成作图）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图，在图a、图b、图c中都有直线m∥n，
    （1）在图a中，∠2和∠1、∠3之间的数量关系是              .
    （2）猜想：在图b中，∠1、∠2、∠3、∠4之间的数量关系是              。
    （3）猜想：在图c中，∠2、∠4和∠1、∠3、∠5的数量关系式是                。

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图，点D、E、F分别在AB、BC、AC上，且DE//AC，EF//AB ，下面写出了证明“∠A+∠B+∠C=180°”的部分过程，请完成填空：

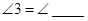    DE // AC，EF // AB  (              )
    ，(             )
    EF // AB.
     (                )
    DE // AC.
     (                 )
     (                )

    .

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图，C是线段AB的中点，D是线段BC的中点，已知图中所有线段的长度之和为39，求线段BC的长.

    查看答案和解析>>

    同步练习册答案