
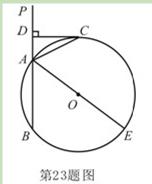
 ,
, 为⊙O的弦,点
为⊙O的弦,点 在
在 上,若
上,若 ,
, ,
, ,则
,则 的长为 .
的长为 .
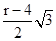 ,结合垂径定理得出BG=5,分别在Rt△OBE中和Rt△OBG中,根据勾股定理列出等式,联立求解即可得出r的值.
,结合垂径定理得出BG=5,分别在Rt△OBE中和Rt△OBG中,根据勾股定理列出等式,联立求解即可得出r的值.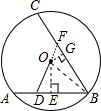
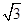 ,
,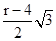 ,
,

科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
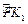 ,
,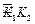 ,
,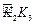 ,
,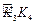 ,
,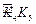 ,
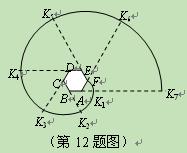
,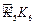 ,……的圆心依次按点A,B,C,D,E,F循环,其弧长分别记为l1,l2,l3,l4,l5,l6,…….当AB=1时,l2 011等于( )
,……的圆心依次按点A,B,C,D,E,F循环,其弧长分别记为l1,l2,l3,l4,l5,l6,…….当AB=1时,l2 011等于( )A.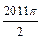 | B.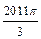 | C.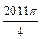 | D.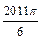 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 的周长为
的周长为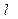 ,面积为S,内切圆
,面积为S,内切圆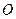 的半径为
的半径为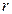 ,探究
,探究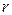 与S、
与S、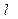 之间的关系.连结
之间的关系.连结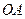 ,
,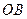 ,
,

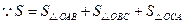
 ,
,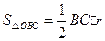 ,
,

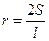
 :
:
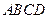 存在内切圆(与各边都相切的圆),如图23—2且面积为
存在内切圆(与各边都相切的圆),如图23—2且面积为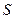 ,各边长分别为
,各边长分别为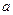 ,
,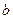 ,
,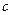 ,
, ,试推导四边形的内切圆半径公式;
,试推导四边形的内切圆半径公式;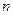 边形(
边形(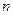 为不小于3的整数)存在内切圆,且面积为
为不小于3的整数)存在内切圆,且面积为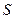 ,各边长分别为
,各边长分别为 ,
,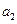 ,
, ,
,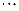 ,
, ,合理猜想其内切圆半径公式(不需说明理由).
,合理猜想其内切圆半径公式(不需说明理由).查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
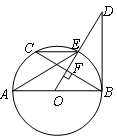
 置关系,并给出证明;
置关系,并给出证明;查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
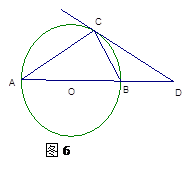
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com