
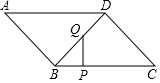
 ��ͼ����?ABCD�У�BC=20$\sqrt{2}$cm��CD=20cm����A=45�㣬����P�ӵ�B��������BC���C�˶�������Q�ӵ�D��������DB���B�˶�����P�͵�Q���˶��ٶȷֱ�Ϊ3$\sqrt{2}$cm/s��2cm/s��һ��ֹͣ�˶�������һ��Ҳ��ֹ֮ͣ������BPQ��ֱ��������ʱ����Ҫ������������
��ͼ����?ABCD�У�BC=20$\sqrt{2}$cm��CD=20cm����A=45�㣬����P�ӵ�B��������BC���C�˶�������Q�ӵ�D��������DB���B�˶�����P�͵�Q���˶��ٶȷֱ�Ϊ3$\sqrt{2}$cm/s��2cm/s��һ��ֹͣ�˶�������һ��Ҳ��ֹ֮ͣ������BPQ��ֱ��������ʱ����Ҫ������������| A�� | 4s | B�� | $\frac{5}{2}$s | C�� | $\frac{5}{2}$s��4s | D�� | 6s |
���� ��ͼ��DH��BC��H������֤����DBC�ǵ���ֱ�������Σ��Ƴ���DBC=45�㣬�Ƴ���BQ=$\sqrt{2}$PB��PB=$\sqrt{2}$BQʱ����BQP��ֱ�������Σ��г����̼��ɽ�����⣮
��� �⣺��ͼ��DH��BC��H��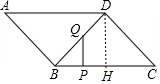
���ı���ABCD��ƽ���ı��Σ�
���C=��A=45�㣬
��DH=CH��
��CD=20��
��DH=CH=10$\sqrt{2}$��
��Rt��DBH��BD=$\sqrt{D{H}^{2}+B{H}^{2}}$=20��
��BD=CD��
���DBC=��C=45�㣬
�൱BQ=$\sqrt{2}$PB��PB=$\sqrt{2}$BQʱ����BQP��ֱ�������Σ�
��20-2t=$\sqrt{2}$��3$\sqrt{2}$t��3$\sqrt{2}$t=$\sqrt{2}$��20-2t����
���t=$\frac{5}{2}$��4s��
��ѡC��
���� ���⿼��ƽ���ı��ε����ʡ�����ֱ�������ε����ʡ����ɶ�����֪ʶ������Ĺؼ���ѧ�����ò������������̽�����⣬�����п��������ͣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
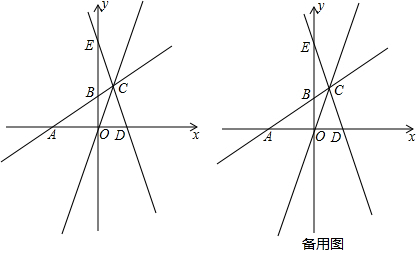
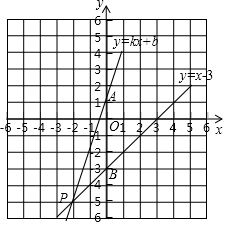 ��ͼ����֪һ�κ���y=kx+b������A��0��1���Һ�ֱ��y=x-3���ڵ�P��a��-5����
��ͼ����֪һ�κ���y=kx+b������A��0��1���Һ�ֱ��y=x-3���ڵ�P��a��-5�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 5 | B�� | 6 | C�� | 7 | D�� | 10 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\left\{\begin{array}{l}{x+y=5}\\{z+x=3}\end{array}\right.$ | B�� | $\left\{\begin{array}{l}{x+\frac{1}{y}=1}\\{\frac{1}{x}-y=3}\end{array}\right.$ | ||
| C�� | $\left\{\begin{array}{l}{x-y+xy=4}\\{3x-y=4}\end{array}\right.$ | D�� | $\left\{\begin{array}{l}{\frac{1}{2}x-2y=15}\\{\frac{1}{3}x+\frac{1}{2}y=4}\end{array}\right.$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
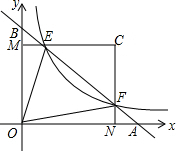 ��ͼ����ƽ��ֱ������ϵ�У�ֱ��AB��x�ᡢy��ֱ��ڵ�A��B���뷴�������� y=$\frac{k}{x}$��kΪ��������k��0���ڵ�һ����ͼ���ڵ�E��F������E��EM��y����M������F��FN��x����N��ֱ��EM��FN���ڵ�C���� $\frac{BE}{BF}$=$\frac{1}{4}$���ǡ�CEF�����Ϊs1����OEF�����Ϊs2���� $\frac{s_1}{s_2}$=��������
��ͼ����ƽ��ֱ������ϵ�У�ֱ��AB��x�ᡢy��ֱ��ڵ�A��B���뷴�������� y=$\frac{k}{x}$��kΪ��������k��0���ڵ�һ����ͼ���ڵ�E��F������E��EM��y����M������F��FN��x����N��ֱ��EM��FN���ڵ�C���� $\frac{BE}{BF}$=$\frac{1}{4}$���ǡ�CEF�����Ϊs1����OEF�����Ϊs2���� $\frac{s_1}{s_2}$=��������| A�� | $\frac{1}{4}$ | B�� | $\frac{1}{2}$ | C�� | $\frac{3}{5}$ | D�� | $\frac{5}{8}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 С����ѧУ�μӱ�ҵ�����ݳ�����ѧУʱ�����ݳ��������ڼ��У���ʱ���ҵ���Ὺʼ����25���ӣ������������лؼң�ͬʱ�������״Ӽ�����������г�����3�����ٶȸ����͵��ߣ�������;��������������С���������������г���ԭ�����ٶ���С������ѧУ��ͼ���߶�AB��OB��ʾ����ǰ���������������͵��ߡ�С��ȡ���߹����У�������ѧУ��·��S���ף�������ʱ��t�֣�֮��ĺ�����ϵ�����ͼ�����������⣮
С����ѧУ�μӱ�ҵ�����ݳ�����ѧУʱ�����ݳ��������ڼ��У���ʱ���ҵ���Ὺʼ����25���ӣ������������лؼң�ͬʱ�������״Ӽ�����������г�����3�����ٶȸ����͵��ߣ�������;��������������С���������������г���ԭ�����ٶ���С������ѧУ��ͼ���߶�AB��OB��ʾ����ǰ���������������͵��ߡ�С��ȡ���߹����У�������ѧУ��·��S���ף�������ʱ��t�֣�֮��ĺ�����ϵ�����ͼ�����������⣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com