Question

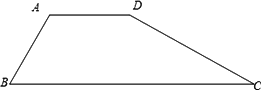
已知梯形ABCD中，AD∥BC，AB＝AD(如图所示)，∠BAD的平分线AE交BC于点E，连接DE．

(1)在下图中，用尺规作∠BAD的平分线AE(保留作图痕迹不写作法)，并证明四边形ABED是菱形．

(2)若∠ABC＝60°，EC＝2BE．求证：ED⊥DC．

Answer 1

答案：
解析：

解答：证明：(1)梯形ABCD中，AD∥BC， 　　∴四边形ABED是平行四边形， 　　又AB＝AD， 　　∴四边形ABED是菱形； 　　(2)∵四边形ABED是菱形，∠ABC＝60°， 　　∴∠DEC＝60°，AB＝ED， 　　又EC＝2BE， 　　∴EC＝2DE， 　　∴△DEC是直角三角形， 　　∴ED⊥DC． 　　点评：本题考查了尺规作图及菱形、直角三角形的性质及判定，综合性较强，锻炼了学生的动手、动脑的能力． 　　考点：梯形；菱形的判定与性质；作图－基本作图． 　　专题：作图题；证明题． 　　分析：(1)根据尺规作图：角的平分线的基本做法，可得到∠BAD的平分线AE；利用菱形的判定定理，即可证得； 　　(2)根据直角三角形的性质定理，可得△EDC是直角三角形，即可得ED⊥DC；