
����Ŀ����ͼ�٣���ABC�У���ABC=45�㣬AH��BC�ڵ�H����D��AH�ϣ���DH=CH������BD��
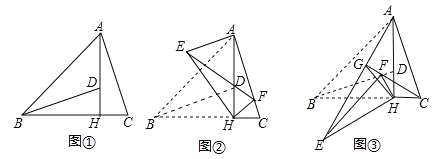
��1����֤��BD=AC��
��2������BHD�Ƶ�H��ת���õ���EHF����B��D�ֱ����E��F��Ӧ��������AE��
����ͼ�ڣ�����F����AC��ʱ����F����C�غϣ�����BC=4��tanC=3����AE�ij���
����ͼ�ۣ�����EHF���ɡ�BHD�Ƶ�H��ʱ����ת30��õ�ʱ��������CF��AE�ཻ�ڵ�G������GH����̽���߶�GH��EF֮������ĵ�����ϵ����˵��������
���𰸡���1��֤������������2����![]() ����
����![]() ��
��![]() ��
��
��������
�����������1�����жϳ�AH=BH�����жϳ���BHD�ա�AHC���ɣ�
��2�����ȸ���tanC=3�����AH=3��CH=1��Ȼ����ݡ�EHA�ա�FHC���õ���HP=3AP��AE=2AP������ù��ɶ������ɣ�
�����жϳ���AGQ�ס�CHQ���õ�![]() ��Ȼ���жϳ���AQC�ס�GQH�������Ʊȼ��ɣ�
��Ȼ���жϳ���AQC�ס�GQH�������Ʊȼ��ɣ�
�����������1����Rt��AHB�У���ABC=45�㣬��AH=BH���ڡ�BHD�͡�AHC�У���AH=BH����BHD=��AHC��DH=CH�����BHD�ա�AHC����BD=AC��
��2������ͼ����Rt��AHC�У���tanC=3����![]() =3����CH=x����BH=AH=3x����BC=4����3x+x=4����x=1����AH=3��CH=1������ת֪����EHF=��BHD=��AHC=90�㣬EH=AH=3��CH=DH=FH�����EHA=��FHC��
=3����CH=x����BH=AH=3x����BC=4����3x+x=4����x=1����AH=3��CH=1������ת֪����EHF=��BHD=��AHC=90�㣬EH=AH=3��CH=DH=FH�����EHA=��FHC��![]() �����EHA�ա�FHC�����EAH=��C����tan��EAH=tanC=3������H��HP��AE����HP=3AP��AE=2AP����Rt��AHP�У�
�����EHA�ա�FHC�����EAH=��C����tan��EAH=tanC=3������H��HP��AE����HP=3AP��AE=2AP����Rt��AHP�У�![]() ����
����![]() ����AP=
����AP=![]() ����AE=
����AE=![]() ��
��
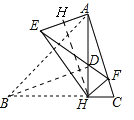
���ɢ��У���AEH�͡�FHC��Ϊ���������Σ����GAH=��HCG=90�㣬���AGQ�ס�CHQ����![]() ����
����![]() ���ߡ�AQC=��GQE�����AQC�ס�GQH����
���ߡ�AQC=��GQE�����AQC�ס�GQH����![]() =sin30��=
=sin30��=![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������������εĶ�Ӧ�߷ֱ���15cm��25cm�����ǵ��ܳ����40cm���������������ε��ܳ��ֱ��ǣ�������
A.75cm��115cmB.60cm��100cmC.85cm��125cmD.45cm��85cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
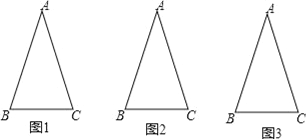
����Ŀ����ͼ����ABC�У�AB=AC����A=36�����������������������Ϊ�ƽ���������Σ���������²���������ͼ��Ҫ��ʹ��Բ�棬����������ָ�ĵ��������θ�������������ABC��
��1����ͼ1�л�1���߶Σ�ʹͼ����2�����������Σ���ֱ��д����2�����������εĶ��Ƕ����ֱ����������������Ⱥ��������������ȣ�
��2����ͼ2�л�2���߶Σ�ʹͼ����4�����������Σ�
��3�����������ϲ������֣�����ABC�л�n���߶Σ���ͼ���������������������������Σ����������������������ƽ���������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ���ı���ABCD�У���A����B����C=2��3��2�����D=(����)
A.36��B.108��C.72��D.60��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD��AD��BC����B��90��AD��6��AB��4��BC��9��
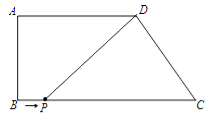
��1����CD�ij���
��2����P�ӵ�B��������ÿ��1����λ���ٶ����ű�BC���C�˶�������DP�����P�˶���ʱ��Ϊt������tΪ��ֵʱ����PDCΪ���������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����23��ʾ�������ǣ�������.
A. ����2��������2��������2�� B. ����2��+����2��+����2��
C. ����2����3 D. ��2��2��2
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com