
【题目】在世界环境日(6月5日),学校组织了保护环境知识测试,现从中随机抽取部分学生的成绩作为样本,按“优秀”“良好”“合格”“不合格”四个等级进行统计,绘制了如下尚不完整的统计图表.
测试成绩统计表
等级 | 频数(人数) | 频率 |
优秀 | 30 |
|
良好 |
| 0.45 |
合格 | 24 | 0.20 |
不合格 | 12 | 0.10 |
合计 |
| 1 |

根据统计图表提供的信息,解答下列问题:
(1)表中![]() ________,
________,![]() ________,
________,![]() ________;
________;
(2)补全条形统计图;
(3)若该校有2400名学生参加了本次测试,估计测试成绩等级在良好以上(包括良好)的学生约有多少人?
科目:初中数学 来源: 题型:
【题目】问题呈现
如图1,在边长为1的正方形网格中,连接格点![]() 、
、![]() 和
和![]() 、
、![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,求
,求![]() 的值.
的值.
方法归纳
求一个锐角的三角函数值,我们往往需要找出(或构造出)一个直角三角形.观察发现问题中![]() 不在直角三角形中,我们常常利用网格画平行线等方法解决此类问题.比如连接格点
不在直角三角形中,我们常常利用网格画平行线等方法解决此类问题.比如连接格点![]() 、
、![]() ,可得
,可得![]() ,则
,则![]() ,连接
,连接![]() ,那么
,那么![]() 就变换到中
就变换到中![]() .
.
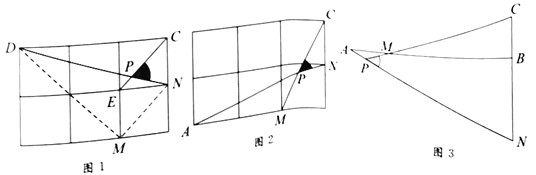
问题解决
(1)直接写出图1中![]() 的值为_________;
的值为_________;
(2)如图2,在边长为1的正方形网格中,![]() 与
与![]() 相交于点
相交于点![]() ,求
,求![]() 的值;
的值;
思维拓展
(3)如图3,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() ,延长
,延长![]() 到
到![]() ,使
,使![]() ,连接
,连接![]() 交
交![]() 的延长线于点
的延长线于点![]() ,用上述方法构造网格求
,用上述方法构造网格求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A的坐标为(0,2),点B的坐标为(1,0),连结AB,以AB为边在第一象限内作正方形ABCD,直线BD交双曲线y═![]() (k≠0)于D、E两点,连结CE,交x轴于点F.
(k≠0)于D、E两点,连结CE,交x轴于点F.

(1)求双曲线y=![]() (k≠0)和直线DE的解析式.
(k≠0)和直线DE的解析式.
(2)求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为边
为边![]() 上的一点(与
上的一点(与![]() 、
、![]() 不重合)四边形
不重合)四边形![]() 关于直线
关于直线![]() 的对称图形为四边形
的对称图形为四边形![]() ,延长
,延长![]() 交
交![]() 与点
与点![]() ,记四边形
,记四边形![]() 的面积为
的面积为![]() .
.
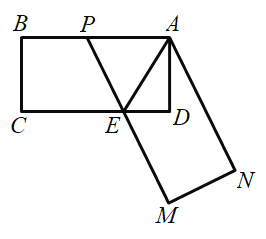
(1)若![]() ,求
,求![]() 的值;
的值;
(2)设![]() ,求
,求![]() 关于
关于![]() 的函数表达式.
的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某旅游景区为方便游客,修建了一条东西走向的木栈道 AB ,栈道 AB 与景区道路CD 平行.在 C 处测得栈道一端 A 位于北偏西 42°方向,在 D 处测得栈道另一端 B 位于北偏西 32°方向.已知 CD =120 m , BD =80 m ,求木栈道 AB 的长度(结果保留整数) .
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,把与
中,把与![]() 轴交点相同的二次函数图像称为“共根抛物线”.如图,抛物线
轴交点相同的二次函数图像称为“共根抛物线”.如图,抛物线![]() 的顶点为
的顶点为![]() ,交
,交![]() 轴于点
轴于点![]() 、
、![]() (点
(点![]() 在点
在点![]() 左侧),交
左侧),交![]() 轴于点
轴于点![]() .抛物线
.抛物线![]() 与
与![]() 是“共根抛物线”,其顶点为
是“共根抛物线”,其顶点为![]() .
.
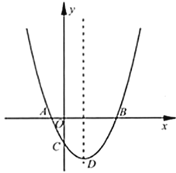
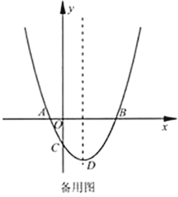
(1)若抛物线![]() 经过点
经过点![]() ,求
,求![]() 对应的函数表达式;
对应的函数表达式;
(2)当![]() 的值最大时,求点
的值最大时,求点![]() 的坐标;
的坐标;
(3)设点![]() 是抛物线
是抛物线![]() 上的一个动点,且位于其对称轴的右侧.若
上的一个动点,且位于其对称轴的右侧.若![]() 与
与![]() 相似,求其“共根抛物线”
相似,求其“共根抛物线”![]() 的顶点
的顶点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了打好疫情期间的复工复产攻坚战,某公司决定为员工采购一批口罩和消毒液,经了解,购买4包口罩和3瓶消毒液共需要185元,购买8包口罩和5瓶消毒液共需要335元,
(1)一包口罩和一瓶消毒液各需要多少元?
(2)实际购买时发现厂家有两种优惠方案:方案一:购买口罩不超过20包时,每包都按九折优惠,超过20包时,超过部分每包按七折优惠;方案二:口罩和消毒液都按原价的八折优惠,公司购买![]() 包口罩,10瓶消毒液.
包口罩,10瓶消毒液.
①求两种方案下所需的费用![]() (单位:元)与
(单位:元)与![]() (单位:包)的函数关系式;
(单位:包)的函数关系式;
②若该公司决定购买![]() 包口罩和10瓶消毒液,请你帮助该公司决定选择哪种方案更合算.
包口罩和10瓶消毒液,请你帮助该公司决定选择哪种方案更合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,AB=5,BC=8,cosB=![]() ,点E是BC边上的动点,以C为圆心,CE长为半径作圆C,交AC于F,连接AE,EF.
,点E是BC边上的动点,以C为圆心,CE长为半径作圆C,交AC于F,连接AE,EF.
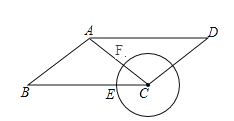
(1)求AC的长;
(2)当AE与圆C相切时,求弦EF的长;
(3)圆C与线段AD没有公共点时,确定半径CE的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某科技有限公司用![]() 万元作为新产品的研发费用,成功研制出了一种市场急需的电子产品,已于当年投人生产并进行销售.已知生产这种电子产品的成本为
万元作为新产品的研发费用,成功研制出了一种市场急需的电子产品,已于当年投人生产并进行销售.已知生产这种电子产品的成本为![]() 元/件,在销售过程中发现:每年的年销售量
元/件,在销售过程中发现:每年的年销售量![]() (万件)与销售价格
(万件)与销售价格![]() (元/件)的关系如图所示,其中
(元/件)的关系如图所示,其中![]() 为反比例函数图象的一部分,
为反比例函数图象的一部分,![]() 为一次函数图象的一部分.设公司销售这种电子产品的年利润为
为一次函数图象的一部分.设公司销售这种电子产品的年利润为![]() (万元).(注意:第一年年利润=电子产品销售收人
(万元).(注意:第一年年利润=电子产品销售收人![]() 电子产品生产成本
电子产品生产成本![]() 研发费用)
研发费用)
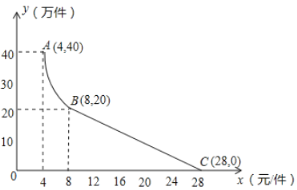
(1)分别写出图中![]() 段、
段、![]() 段
段![]() (万件)与
(万件)与![]() (元/件)之间的函数关系式,并写出自变量的取值范围;
(元/件)之间的函数关系式,并写出自变量的取值范围;
(2)求出第一年这种电子产品的年利润![]() (万元)与
(万元)与![]() (元/件)之间的函数关系式;
(元/件)之间的函数关系式;
(3)求该公司第一年年利润的最大值, 并说明利润最大时是盈利还是亏损,盈利或亏损多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com