
【题目】如图,△ABC的两条中线BD、CE交于点F.
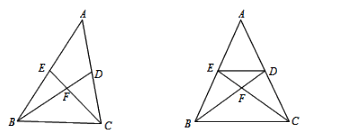
![]()
(1)![]() = _______;
= _______;
(2)若BE2 = EFEC,且![]() =
= ![]() ,EF =
,EF =![]() ,求DE的长;
,求DE的长;
【答案】(1)![]() ;(2)2
;(2)2![]() .
.
【解析】
(1)由BD、CE为△ABC的两条中线,则ED∥BC,ED=![]() BC,则△EFD∽△CFB,则
BC,则△EFD∽△CFB,则![]() 即可完成解答.
即可完成解答.
(2)由(1)得![]() ,由EF=
,由EF=![]() ,则FC=2
,则FC=2![]() ,EC=3
,EC=3![]() ;又由BE2 = EFEC得
;又由BE2 = EFEC得![]() ,结合∠BEF=∠BEF,证得△BEF∽△ECB,可知
,结合∠BEF=∠BEF,证得△BEF∽△ECB,可知![]() ,进而求得DE;
,进而求得DE;
解:(1)∵BD、CE为△ABC的两条中线
∴ED∥BC,ED=![]() BC
BC
∴△EFD∽△CFB
∴![]() ,
,
故答案为![]() ;
;
(2)∵EF=![]()
∴FC=2![]() ,EC=3
,EC=3![]()
又∵BE2 = EFEC=18
∴![]() ,BE=3
,BE=3![]() ,BF=2DF=4
,BF=2DF=4![]()
又∵∠BEF=∠BEF
∴△BEF∽△ECB(两边对应成比例且夹角相等的三角形相似)
∴![]()
∴BC=4![]() , ED=
, ED=![]() BC=2
BC=2![]() .
.


 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,CA=CB,∠ACB=90°,AB=2,点D为AB的中点,以点D为圆心作圆,半圆恰好经过△ABC的直角顶点C,以点D为顶点,作∠EDF=90°,与半圆交于点E、F,则图中阴影部分的面积是_______.
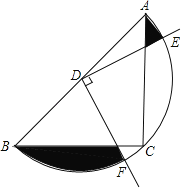
查看答案和解析>>
科目:初中数学 来源: 题型:
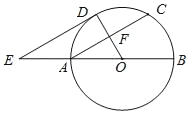
【题目】如图,AB为⊙O的直径,F为弦AC的中点,连接OF并延长交弧AC于点D,过点D作⊙O的切线,交BA的延长线于点E.
(1)求证:AC∥DE;
(2)连接AD、CD、OC.填空
①当∠OAC的度数为 时,四边形AOCD为菱形;
②当OA=AE=2时,四边形ACDE的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
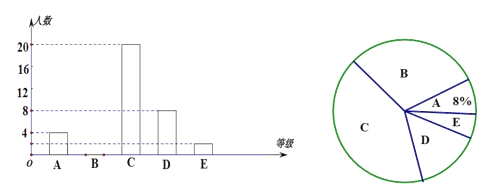
【题目】2020的寒假是一个特殊的假期.由于“新型冠状肺炎病毒”影响,学校的开学日期不断延后,在这期间某中学在学校微信公众号上积极鼓励学生静在家中沉下心来参加“静读名著”活动,活动以读名著的本书多少设为A,B,C,D,E五个等级,(本数依次为5,4,3,2,1),该校八(3)班全体学生参加了这次静在家中沉下心来读名著活动,芳芳同学通过调查并将这次读书阅读本数的结果绘制成如下两幅不完整的统计图.请根据图中信息,解答下列问题:
(1)该校八(3)班共有______学生;
(2)扇形统计图中B等级所对应扇形的圆心角等于______度;
(3)补全条形统计图;
(4)若该校有学生2500人读名著的本书在B、C级的人数一共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,AC是⊙O的一条弦,D为弧BC的中点,作DE⊥AC,垂足为AC的延长线上的点E,连接DA,DB.
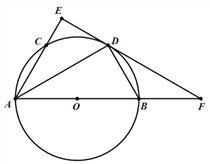
(1)求证:DE为⊙O的切线;
(2)试探究线段AB,BD,CE之间的数量关系,并说明理由;
(3)延长ED交AB的延长线于F,若AD=DF,DE=![]() ,求⊙O的半径;
,求⊙O的半径;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形 ABCD 中,AD∥BC,AB=BC,对角线 AC、BD 交于点 O,BD 平分∠ABC,过点 D 作 DE⊥BC 交 BC 的延长线于点 E.连接 OE.
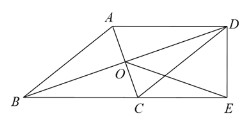
(1)求证:四边形 ABCD 是菱形;
(2)若 tan∠DBC=![]() ,AB=
,AB=![]() ,求线段 OE 的长.
,求线段 OE 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
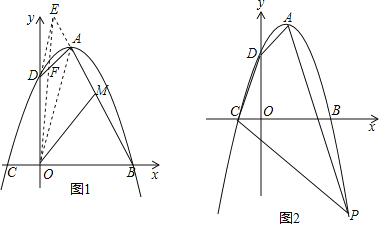
【题目】在平面直角坐标系xOy中,顶点为A的抛物线与x轴交于B、C两点,与y轴交于点D,已知A(1,4),B(3,0).
(1)求抛物线对应的二次函数表达式;
(2)探究:如图1,连接OA,作DE∥OA交BA的延长线于点E,连接OE交AD于点F,M是BE的中点,则OM是否将四边形OBAD分成面积相等的两部分?请说明理由;
(3)应用:如图2,P(m,n)是抛物线在第四象限的图象上的点,且m+n=﹣1,连接PA、PC,在线段PC上确定一点M,使AN平分四边形ADCP的面积,求点N的坐标.提示:若点A、B的坐标分别为(x1,y1)、(x2,y2),则线段AB的中点坐标为(![]() ,
,![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有一列数a1,a2,a3,…,a98,a99,a100,其中a3=2020,a7=-2018,a98=-1,且满足任意相邻三个数的和为常数,则a1+a2+a3+…+a98+a99+a100的值为( )
A.1985B.-1985C.2019D.-2019
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com