
 如图,已知直线AB∥直线CD,点E,F分别在直线AB和CD上,EN∥MF,HE∥FN,若∠N=114°,HE平分∠AEN,则∠MFH的度数为( )
如图,已知直线AB∥直线CD,点E,F分别在直线AB和CD上,EN∥MF,HE∥FN,若∠N=114°,HE平分∠AEN,则∠MFH的度数为( )| A. | 48° | B. | 58° | C. | 66° | D. | 68° |
分析 根据已知条件得到四边形EMFN是平行四边形,根据平行四边形的性质得到∠NEM=66°,根据角平分线的性质得到∠AEH=∠NEM=66°,根据平行线的性质得到∠AEH=∠MHF=∠NEM=∠HMF=66°,根据三角形的内角和即可得到结论.
解答 解:∵EN∥MF,HE∥FN,
∴四边形EMFN是平行四边形,
∵∠N=114°,
∴∠NEM=66°,
∵HE平分∠AEN,
∴∠AEH=∠NEM=66°,
∵直线AB∥直线CD,
∴∠AEH=∠MHF=∠NEM=∠HMF=66°,
∴∠MFH=180°-66°-66°=48°,故选A.
点评 本题考查的是平行线的性质,用到的知识点为:两直线平行,同旁内角互补,熟练掌握平行线的性质定理是解题的关键.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案科目:初中数学 来源: 题型:解答题
 补全下列各题解题过程.
补全下列各题解题过程.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
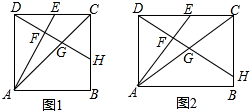
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
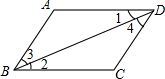 如图,下列推理是否正确,请写出你认为是正确推理的编号①②④.
如图,下列推理是否正确,请写出你认为是正确推理的编号①②④.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{20}$和$\sqrt{5}$ | B. | $\sqrt{12}$和$\sqrt{27}$ | C. | $\sqrt{\frac{1}{3}}$或$\sqrt{\frac{2}{3}}$ | D. | $\sqrt{45a}$和$\sqrt{125a}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
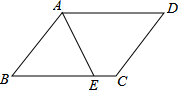 如图,平行四边形ABCD的周长为20cm,AE平分∠BAD,若CE=2cm,则AB的长度是( )
如图,平行四边形ABCD的周长为20cm,AE平分∠BAD,若CE=2cm,则AB的长度是( )| A. | 10cm | B. | 8cm | C. | 6cm | D. | 4cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
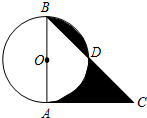 如图,在⊙O中,直径AB=2,CA切⊙O于A,BC交⊙O于D,若∠C=45°,则图中阴影部分的面积为( )
如图,在⊙O中,直径AB=2,CA切⊙O于A,BC交⊙O于D,若∠C=45°,则图中阴影部分的面积为( )| A. | $\frac{π}{2}$ | B. | 2 | C. | π | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com