
分析 (1)根据题意,先求出2013年全校的学生人数就可以求出2014年的学生人数;
(2)①设2012人均阅读量为x本,则2013年的人均阅读量为(x+1)本,根据阅读总量之间的数量关系建立方程就可以得出结论;
②由①的结论就可以求出2012年读书社的人均读书量,2014年读书社的人均读书量,全校的人均读书量,由2014年读书社的读书量与全校读书量之间的关系建立方程求出其解即可.
解答 解:(1)由题意,得
2014年全校学生人数为:1000×(1+10%)=1100人,
故2015年全校学生人数为:1100+100=1200人;
(2)①设2013人均阅读量为x本,则2014年的人均阅读量为(x+1)本,由题意,得
1100(x+1)=1000x+1700,
解得:x=6.
答:2013年全校学生人均阅读量为6本;
②由题意,得
2013年读书社的人均读书量为:2.5×6=15本,
2015年读书社人均读书量为15(1+a)2本,
2015年全校学生的人均读书量为6(1+a)本,
80×15(1+a)2=1200×6(1+a)×25%
2(1+a)2=3(1+a),
∴a1=-1(舍去),a2=0.5.
答:a的值为0.5.
点评 本题考查了列一元一次方程解实际问题的运用,一元二次方程的解法的运用,增长率问题的数量关系的运用,解答时根据阅读总量之间的关系建立方程是关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
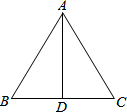 AD是△ABC的角平分线,过点D作DE⊥AB于E,DF⊥AC于F,则下列结论不一定正确的是( )
AD是△ABC的角平分线,过点D作DE⊥AB于E,DF⊥AC于F,则下列结论不一定正确的是( )| A. | DE=DF | B. | BD=CD | C. | AE=AF | D. | ∠ADE=∠ADF |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com