
如图,圆内接四边形ABDC,AB是⊙O的直径,OD⊥BC于E.
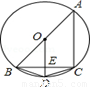
(1)求证:∠BCD=∠CBD;
(2)若BE=4,AC=6,求DE的长.
(1)详见解析;(2)2.
【解析】
试题分析:(1)由题目条件OD⊥BC于E,可知OD平分弧BC(垂径定理),即弧BD=弧CD,∠BCD是弧BD所对的圆周角,∠CBD是弧CD所对的圆周角,由圆周角定理,同弧或等弧所对的圆周角相等可以得到∠BCD=∠CBD;(2) 由题目条件OD⊥BC于E,可知OD平分弦BC(垂径定理),即BE= CE=4,所以BC=8,因为AB是⊙O的直径,所以∠C为直角,在Rt△ACB中,AC=6,BC=8,由勾股定理,AB=10,OB=5,在Rt△OEB中,OB=5,BE=4,由勾股定理,OE=3,DE=OD-OE=2.
试题解析:(1)∵OD⊥BC于E,
∴OD平分弧BC(垂径定理),即弧BD=弧CD,
又∵∠BCD是弧BD所对的圆周角,∠CBD是弧CD所对的圆周角,
由圆周角定理知∠BCD=∠CBD.
(2) ∵OD⊥BC于E,
∴OD平分弦BC(垂径定理),即BE= CE=4,BC=8,
∵AB是⊙O的直径,
∴∠C为直角,
在Rt△ACB中,AC=6,BC=8,由勾股定理,AB=10,OB=5,
在Rt△OEB中,OB=5,BE=4,由勾股定理,OE=3,DE=OD-OE=2.
考点:1.圆周角定理和垂径定理;2.垂径三角形三边的关系.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com