
如图所示,已知:AB是⊙O的直径,弦CD⊥AB,垂足为M,弦AE与CD相交于点F,则有结论AD2=AE·AF成立(为什么?).

(1)若将弦CD向下平移至与⊙O相切于点B时(如图所示),AE·AF是否等于AG2?如果不相等,请探求AE·AF等于哪两条线段的积?并给出证明.

(2)当CD继续向下平移至与⊙O相离时(如图所示),在(1)中探求的结论是否还成立?并说明理由.

|
证明:连接DE. 因为CD⊥AB,AB是直径, 所以 所以∠ADC=∠AED. 又因为∠DAF=∠EAD, 所以△ADF∽△AED, 所以 所以AD2=AE·AF. (1)AE·AF不等于AG2,应该有结论AE·AF=AG·AH. 证明:连接BE,BG. 因为AB是直径,AB⊥CD, 所以∠AEB=∠AGB=∠ABF=∠ABH= 因为∠AEB=∠ABF,∠BAE=∠FAB, 所以△ABE∽△AFB, 所以 所以AE·AF=AB2. 同理可证AG·AH=AB2. 所以AE·AF=AG·AH. (2)在(1)中探求的结论还成立.证明如下: 连接EG,BG. 因为AB是直径,AB⊥CD于M, 所以∠AGB=∠AMF= 所以∠AFM+∠FAM=∠AGE+∠BGE= 因为∠FAM=∠BGE, 所以∠AFM=∠AGE. 又∠FAH=∠GAE, 所以△AFH∽△AGE, 所以 所以AE·AF=AG·AH. |


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:初中数学 来源: 题型:
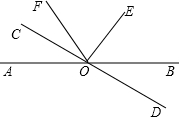 如图所示,已知直线AB和CD相交于点O,∠COE是直角,0F平分∠AOE.∠COF=34°.
如图所示,已知直线AB和CD相交于点O,∠COE是直角,0F平分∠AOE.∠COF=34°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com