
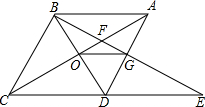
 如图,在菱形ABCD中,∠BAC=60°,AC与BC交于点O,E为CD延长线上的一点,且CD=DE,连接BE分别交AC、AD于点F、G,连接OG,则下列结论中一定成立的是①④.(把所有正确结论的序号都填在横线上)
如图,在菱形ABCD中,∠BAC=60°,AC与BC交于点O,E为CD延长线上的一点,且CD=DE,连接BE分别交AC、AD于点F、G,连接OG,则下列结论中一定成立的是①④.(把所有正确结论的序号都填在横线上)分析 由AAS证明△ABG≌△DEG,得出AG=DG,证出OG是△ACD的中位线,得出OG=$\frac{1}{2}$CD=$\frac{1}{2}$AB,①正确;
先证明四边形ABDE是平行四边形,证出△ABD、△BCD是等边三角形,得出AB=BD=AD,因此OD=AG,得出四边形ABDE是菱形,④正确;
由菱形的性质得得出△ABG≌△BDG≌△DEG,由SAS证明△ABG≌△DCO,得出△ABO≌△BCO≌△CDO≌△AOD≌△ABG≌△BDG≌△DEG,得出②不正确;
证出OG是△ABD的中位线,得出OG∥AB,OG=$\frac{1}{2}$AB,得出△GOD∽△ABD,△ABF∽△OGF,由相似三角形的性质和面积关系得出S四边形ODGF=S△ABF;③不正确;即可得出结果.
解答 解:∵四边形ABCD是菱形,
∴AB=BC=CD=DA,AB∥CD,OA=OC,OB=OD,AC⊥BD,
∴∠BAG=∠EDG,△ABO≌△BCO≌△CDO≌△AOD,
∵CD=DE,
∴AB=DE,
在△ABG和△DEG中,$\left\{\begin{array}{l}{∠BAG=∠EDG}&{\;}\\{∠AGB=∠DGE}&{\;}\\{AB=DE}&{\;}\end{array}\right.$,
∴△ABG≌△DEG(AAS),
∴AG=DG,
∴OG是△ACD的中位线,
∴OG=$\frac{1}{2}$CD=$\frac{1}{2}$AB,①正确;
∵AB∥CE,AB=DE,
∴四边形ABDE是平行四边形,
∵∠BCD=∠BAD=60°,
∴△ABD、△BCD是等边三角形,
∴AB=BD=AD,∠ODC=60°,
∴OD=AG,四边形ABDE是菱形,④正确;
∴AD⊥BE,
由菱形的性质得:△ABG≌△BDG≌△DEG,
在△ABG和△DCO中,$\left\{\begin{array}{l}{OD=AG}&{\;}\\{∠ODC=∠BAG=60°}&{\;}\\{AB=DC}&{\;}\end{array}\right.$,
∴△ABG≌△DCO(SAS),
∴△ABO≌△BCO≌△CDO≌△AOD≌△ABG≌△BDG≌△DEG,②不正确;
∵OB=OD,AG=DG,
∴OG是△ABD的中位线,
∴OG∥AB,OG=$\frac{1}{2}$AB,
∴△GOD∽△ABD,△ABF∽△OGF,
∴△GOD的面积=$\frac{1}{4}$△ABD的面积,△ABF的面积=△OGF的面积的4倍,AF:OF=2:1,
∴△AFG的面积=△OGF的面积的2倍,
又∵△GOD的面积=△AOG的面积=△BOG的面积,
∴S四边形ODGF=S△ABF;不正确;
正确的是①④.
故答案为:①④.
点评 本题考查了菱形的判定与性质、全等三角形的判定与性质、等边三角形的判定与性质、三角形中位线定理、相似三角形的判定与性质等知识;本题综合性强,难度较大.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某校计划组织师生共300人参加一次大型公益活动,如果租用6辆大客车和5辆小客车恰好全部坐满.已知每辆大客车的乘客座位数比小客车多17个.
某校计划组织师生共300人参加一次大型公益活动,如果租用6辆大客车和5辆小客车恰好全部坐满.已知每辆大客车的乘客座位数比小客车多17个.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,菱形ABCD中,∠BAD=45°,E,F,P分别是AB,BC,AC上的动点,PE+PF的最小值等于2,则AB=2$\sqrt{2}$.
如图,菱形ABCD中,∠BAD=45°,E,F,P分别是AB,BC,AC上的动点,PE+PF的最小值等于2,则AB=2$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
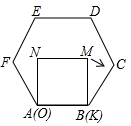 已知正方形MNOK和正六边形ABCDEF边长均为1,把正方形放在正六边形中,使OK边与AB边重合,如图所示,按下列步骤操作:
已知正方形MNOK和正六边形ABCDEF边长均为1,把正方形放在正六边形中,使OK边与AB边重合,如图所示,按下列步骤操作:| A. | 1.4 | B. | 1.1 | C. | 0.8 | D. | 0.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
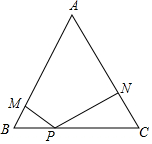 在边长为2的等边三角形ABC中,P是BC边上任意一点,过点 P分别作 PM⊥A B,PN⊥AC,M、N分别为垂足.
在边长为2的等边三角形ABC中,P是BC边上任意一点,过点 P分别作 PM⊥A B,PN⊥AC,M、N分别为垂足.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,-4),B(3,-3),C(1,-1).
如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,-4),B(3,-3),C(1,-1).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com