
 如图,已知正方形ABCD的边长为2,中心为点O,现有边长大小不确定的正方形EFGH,中心也为点O,可绕点O任意旋转,在旋转过程中,正方形EFGH始终在正方形ABCD内(包括正方形的边),当正方形EFGH边长最大时,BE的最小值为$\sqrt{2}$-1.
如图,已知正方形ABCD的边长为2,中心为点O,现有边长大小不确定的正方形EFGH,中心也为点O,可绕点O任意旋转,在旋转过程中,正方形EFGH始终在正方形ABCD内(包括正方形的边),当正方形EFGH边长最大时,BE的最小值为$\sqrt{2}$-1. 分析 由于正方形EFGH始终在正方形ABCD内(包括正方形的边),则正方形EFGH边长最大时,正方形EFGH四个顶点分别在正方形ABCD的各边上,易得正方形EFGH的对角线EG=BC=2,所以OE=1,然后利用两正方形的对角线共线,且点B、E在点O的同侧时,确定BE的值最小.
解答 解:当正方形EFGH边长最大时,正方形EFGH四个顶点分别在正方形ABCD的各边上,此时正方形EFGH的对角线EG=BC=2,所以OE=1,
当对角线EG旋转到BD上且点B、E在点O的同侧时,BE的值最小,最小值=OB-OE=$\sqrt{2}$-1.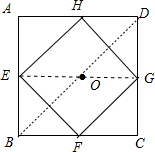
故答案为$\sqrt{2}$-1.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.解决本题的关键是确定正方形EFGH边长的最大值.


科目:初中数学 来源: 题型:选择题
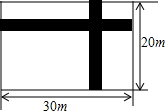 如图,在宽为20米,长为30米的矩形地面上修建两条同样宽为x米的道路,余下部分作为耕地,则耕地面积表示为( )
如图,在宽为20米,长为30米的矩形地面上修建两条同样宽为x米的道路,余下部分作为耕地,则耕地面积表示为( )| A. | (30-x)(20-x)-x2 | B. | (30-x)(20-x) | C. | (30-2x)(20-2x) | D. | (30-2x)(20-x) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在Rt△ABC中,∠C=90°,∠A=30°,点P在AC边上,以点P为中心,将△ABC顺时针旋转90°,得到△DEF,DE交边AC于G,当P为中点时,AG:DG的值为$\frac{\sqrt{3}-1}{2}$.
如图,在Rt△ABC中,∠C=90°,∠A=30°,点P在AC边上,以点P为中心,将△ABC顺时针旋转90°,得到△DEF,DE交边AC于G,当P为中点时,AG:DG的值为$\frac{\sqrt{3}-1}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,正方形ABCD边长为4个单位,两动点P、Q分别从点A、B处,以1单位/s、2单位/s的速度逆时针沿边移动.记移动的时间为x(s),△PBQ面积为y(平方单位),当点Q移动一周又回到点B终止,则y与x的函数关系图象为( )
如图,正方形ABCD边长为4个单位,两动点P、Q分别从点A、B处,以1单位/s、2单位/s的速度逆时针沿边移动.记移动的时间为x(s),△PBQ面积为y(平方单位),当点Q移动一周又回到点B终止,则y与x的函数关系图象为( )| A. | 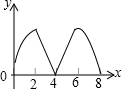 | B. | 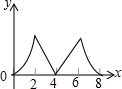 | C. |  | D. | 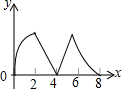 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4000元,8000元 | B. | 8000元,4000元 | C. | 14000元,8000元 | D. | 10000元,12000元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com