
【题目】甲、乙两地相距300千米,一辆货车和一辆轿车分别从甲地开往乙地![]() 轿车的平均速度大于货车的平均速度
轿车的平均速度大于货车的平均速度![]() ,如图,线段OA、折线BCD分别表示两车离甲地的距离
,如图,线段OA、折线BCD分别表示两车离甲地的距离![]() 单位:千米
单位:千米![]() 与时间
与时间![]() 单位:小时
单位:小时![]() 之间的函数关系.
之间的函数关系.
![]() 线段OA与折线BCD中,______表示货车离甲地的距离y与时间x之间的函数关系.
线段OA与折线BCD中,______表示货车离甲地的距离y与时间x之间的函数关系.
![]() 求线段CD的函数关系式;
求线段CD的函数关系式;
![]() 货车出发多长时间两车相遇?
货车出发多长时间两车相遇?

【答案】(1)线段OA表示货车货车离甲地的距离y与时间x之间的函数关系;(2)![]() ;(3)货车出发
;(3)货车出发![]() 小时两车相遇.
小时两车相遇.
【解析】
(1)根据题意可以分别求得两个图象中相应函数对应的速度,从而可以解答本题;
(2)设CD段的函数解析式为y=kx+b,将C(2.5,80),D(4.5,300)两点的坐标代入,运用待定系数法即可求解;
(3)根据题意可以求得OA对应的函数解析式,从而可以解答本题.
![]() 线段OA表示货车货车离甲地的距离y与时间x之间的函数关系,
线段OA表示货车货车离甲地的距离y与时间x之间的函数关系,
理由:![]() 千米
千米![]() 时
时![]() ,
,![]() ,
,
![]() ,轿车的平均速度大于货车的平均速度,
,轿车的平均速度大于货车的平均速度,
![]() 线段OA表示货车离甲地的距离y与时间x之间的函数关系,
线段OA表示货车离甲地的距离y与时间x之间的函数关系,
故答案为:OA;
![]() 设CD段函数解析式为
设CD段函数解析式为![]() ,
,
![]() ,
,![]() 在其图象上,
在其图象上,
![]() ,解得
,解得![]() ,
,
![]() 段函数解析式:
段函数解析式:![]() ;
;
![]() 设线段OA对应的函数解析式为
设线段OA对应的函数解析式为![]() ,
,
![]() ,得
,得![]() ,
,
即线段OA对应的函数解析式为![]() ,
,
![]() ,解得
,解得![]() ,
,
即货车出发![]() 小时两车相遇.
小时两车相遇.


科目:初中数学 来源: 题型:
【题目】甲、乙两人先后从公园大门出发,沿绿道向码头步行,乙先到码头并在原地等甲到达.图1是他们行走的路程y(m)与甲出发的时间x(min)之间的函数图象.
(1)求线段AC对应的函数表达式;
(2)写出点B的坐标和它的实际意义;
(3)设d(m)表示甲、乙之间的距离,在图2中画出d与x之间的函数图象(标注必要数据).

查看答案和解析>>
科目:初中数学 来源: 题型:
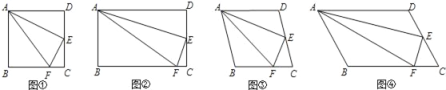
【题目】小明在研究正方形的有关问题时发现有这样一道题:“如图①,在正方形ABCD中,点E是CD的中点,点F是BC边上的一点,且∠FAE=∠EAD.你能够得出什么样的正确的结论?”
(1)小明经过研究发现:EF⊥AE.请你对小明所发现的结论加以证明;
(2)小明之后又继续对问题进行研究,将“正方形”改为“矩形”、“菱形”和“任意平行四边形”(如图②、图③、图④),其它条件均不变,认为仍然有“EF⊥AE”.你同意小明的观点吗?若你同意小明的观点,请取图③为例加以证明;若你不同意小明的观点,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB∥CD,∠1=∠2,DB=DC.
(1)求证:△ABD≌△EDC;
(2)若∠A=135°,∠BDC=30°,求∠BCE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图线段AB和CD表示两面镜子,且直线AB∥直线CD,光线EF经过镜子AB反射到镜予CD,最后反射到光线GH.光线反射时,∠1=∠2,∠3=∠4,下列结论:①直线EF平行于直线GH;②∠FGH的角平分线所在的直线垂直于直线AB;③∠BFE的角平分线所在的直线垂直于∠4的角平分线所在的直线;④当CD绕点G顺时针旋转90时,直线EF与直线GH不一定平行,其中正确的是( )

A. ①②③④B. ①②③C. ②③D. ①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知点E和点F分别在直线AB和CD上,EL和FG分别平分∠BEF和∠EFC,EL∥FG.
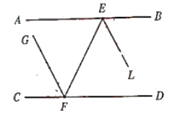
(1)求证:AB∥CD;
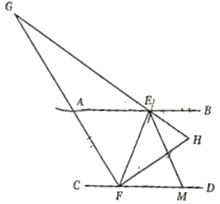
(2)如图,点M为FD上一点,∠BEM,∠EFD的角平分线EH,FH相交于点H,若∠H=∠FEM+15°,延长HE交FG于G点,求∠G的度数;
(3)如图,点N在直线AB和直线CD之间,且EN⊥FN,点P为直线AB上的点,若∠EPF,∠PFN的角平分级交于点Q,设∠BEN=α,直接写出∠PQF的大小为(用含α的式子表示).
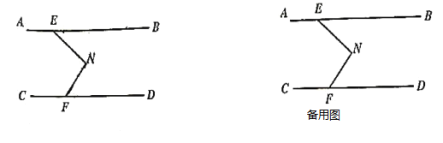
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠BAC=60°,点O为Rt△ABC斜边AB上的一点,以OA为半径的⊙O与BC切于点D,与AC交于点E,连接AD.
(1)求∠CAD的度数;
(2)若OA = 2,求阴影部分的面积(结果保留π).
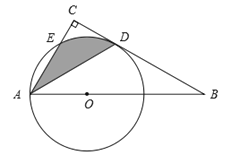
【答案】(1)∠CAD的度数为30°;
(2)阴影部分的面积为![]() .
.
【解析】试题分析:(1)连接OD.由切线的性质可知OD⊥BC,从而可证明AC∥OD,由平行线的性质和等腰三角形的性质可证明∠CAD=∠OAD;(2)连接OE,ED、OD.先证明ED∥AO,然后依据同底等高的两个三角形的面积相等可知S△AED=S△EDO,于是将阴影部分的面积可转化为扇形EOD的面积求解即可.
试题解析:(1)连接OD,
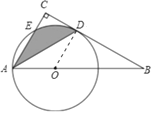
∵BC是⊙O的切线,D为切点,
∴OD⊥BC.
又∵AC⊥BC,
∴OD∥AC,
∴∠ADO=∠CAD.
又∵OD=OA,
∴∠ADO=∠OAD,
∴∠CAD=∠OAD=30°.
(2)连接OE,ED.

∵∠BAC=60°,OE=OA,
∴△OAE为等边三角形,
∴∠AOE=60°,
∴∠ADE=30°.
又∵![]() ,
,
∴∠ADE=∠OAD,
∴ED∥AO,
∴![]()
∴阴影部分的面积 = ![]() .
.
【题型】解答题
【结束】
6
【题目】如图是由两个长方体组合而成的一个立体图形的三视图,根据图中所标尺寸(单位:mm),求这个立体图形的表面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线BG于G点,DE⊥DF,交AB于点E,连结EG、EF.

(1)求证:BG=CF.
(2)请你判断BE+CF与EF的大小关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, ∠B、∠D的两边分别平行。
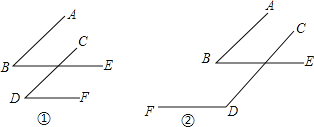
(1)在图1中,∠B与∠D的数量关系是 ;在图2中,∠B与∠FDC的数量关系是 ;
(2)用一句话归纳的结论为: ;
(3)已知∠α的两边与∠β的两边分别平行,并且∠α比∠β的3倍少![]() ,求∠α、∠β的度数.
,求∠α、∠β的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com