
【题目】阅读下面材料,并解决有关问题
我们知道:
|a|=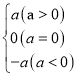
现在我们可以用这一结论来化解含有绝对值的代数式
如化简代数式|x+1|+|x﹣2|时,可令x+1=0和x﹣2=0,分别求得x=﹣1和x=2(称﹣1,2分别为|x+1|和|x﹣2|的零点值)
在实数范围内,零点值x=﹣1和x=2可将全体实数分成不重复且不遗漏的如下三种情况:
(1)x<﹣1(2)﹣1≤x<2(3)x≥2
从而化简代数式|x+1|+|x﹣2|,可分以下三种情况
(1)x<﹣1时,原式=﹣(x+1)﹣(x﹣2)=﹣2x+1
(2)﹣1≤x<2时,原式=x+1﹣(x﹣2)=3
(3)x≥2时,原式=x+1+x﹣2=2x﹣1
通过以上阅读,请你解决以下问题
(1)化简代数式|x+2|+|x﹣4|
(2)求|x﹣1|﹣4|x+1|的最大值.
【答案】(1)当x<﹣2时,|x+2|+|x﹣4|=﹣2x+2;当﹣2≤x<4时,|x+2|+|x﹣4|=6;当x≥4时,|x+2|+|x﹣4|=2x﹣2;(2)2.
【解析】
(1)分为x<﹣2、﹣2≤x<4、x≥4三种情况化简即可;
(2)分x<﹣1、﹣1≤x≤1、x>1分别化简,结合x的取值范围确定代数式值的范围,从而求出代数式的最大值.
解:(1)当x<﹣2时,|x+2|+|x﹣4|=﹣x﹣2+4﹣x=﹣2x+2;
当﹣2≤x<4时,|x+2|+|x﹣4|=x+2+4﹣x=6;
当x≥4时,|x+2|+|x﹣4|=x+2+x﹣4=2x﹣2;
(2)当x<﹣1时,原式=3x+5<2,
当﹣1≤x≤1时,原式=﹣5x﹣3,﹣8≤﹣5x﹣3≤2,
当x>1时,原式=﹣3x﹣5<﹣8,
则|x﹣1|﹣4|x+1|的最大值为2.


 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,点D、E分别在BC、AC上,且BD=CE,连接AD,BE交于点F;
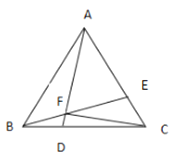
(1)求∠AFE的度数;
(2)连接FC,若∠AFC=90°,BF=1,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=![]() .下列结论:①△APD≌△AEB;②点B到直线AE的距离为
.下列结论:①△APD≌△AEB;②点B到直线AE的距离为![]() ;③EB⊥ED;④S△APD+S△APB=1+
;③EB⊥ED;④S△APD+S△APB=1+![]() ;⑤S正方形ABCD=4+
;⑤S正方形ABCD=4+![]() .其中正确结论的序号是( )
.其中正确结论的序号是( )

A.①③④ B.①②⑤ C.③④⑤ D.①③⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,连接DE交AC于点F.

(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.
(3)在(2)的条件下,若AB=AC=2![]() ,求正方形ADCE周长.
,求正方形ADCE周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图是由一些火柴棒搭成的图案:
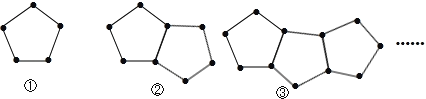
(1)摆第①个图案用 根火柴棒,摆第②个图案用 根火柴棒,摆第③个图案用 根火柴棒.
(2)按照这种方式摆下去,摆第n个图案用多少根火柴棒?
(3)计算一下摆121根火柴棒时,是第几个图案?
查看答案和解析>>
科目:初中数学 来源: 题型:
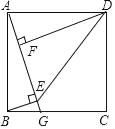
【题目】如图,正方形ABCD中,G为BC边上一点,BE⊥AG于E,DF⊥AG于F,连接DE.
(1)求证:△ABE≌△DAF;
(2)若AF=1,四边形ABED的面积为6,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是等边三角形,D为边AC的中点,AE⊥EC,BD=EC.
(1)求证:△BDA≌△CEA;
(2)请判断△ADE是什么三角形,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
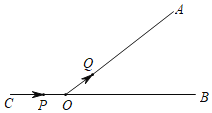
【题目】如图,∠AOB=60°,C是BO延长线上一点,OC=12cm,动点P从点C出发沿CB以2cm/s的速度移动,动点Q从点O出发沿OA以1cm/s的速度移动,如果点P、Q同时出发,用t(s)表示移动的时间,当t=_____s时,△POQ是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
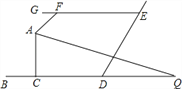
【题目】如图,BD∥GE,AQ 平分∠FAC,交 BD 于 Q,∠GFA=50°,∠Q=25°,则∠ACB 的 度数( )
A. 90° B. 95° C. 100° D. 105°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com