
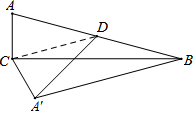
 如图,在△ACB中,∠ACB=90°,∠A=75°,点D是AB的中点.将△ACD沿CD翻折得到△A′CD,连接A′B.
如图,在△ACB中,∠ACB=90°,∠A=75°,点D是AB的中点.将△ACD沿CD翻折得到△A′CD,连接A′B.分析 (1)依据直角三角形斜边上中线的性质可知CD=AD,然后依据等腰三角形的性质和三角形的内角和定理可求得∠ADC=30°,由翻折的性质可知∠CDA′=30°,从而可求得∠A′DB的度数,然后依据DA′=DB可求得∠DBA′=30°,从而可证明CD∥A′B;
(2)连结AA′,先证明△ADA′为等边三角形,从而可得到∠AA′D=60°,然后可求得∠AA′B=90°,最后依据勾股定理求解即可.
解答 解:(1)∵∠ACB=90°,点D是AB的中点
∴AD=BD=CD=$\frac{1}{2}$AB.
∴∠ACD=∠A=75°.
∴∠ADC=30°.
∵△A′CD由△ACD沿CD翻折得到,
∴△A′CD≌△ACD.
∴AD=AD,∠A′DC=∠ADC=30°.
∴AD=A′D=DB,∠ADA′=60°.
∴∠A′DB=120°.
∴∠DBA′=∠DA′B=30°.
∴∠ADC=∠DBA'.
∴CD∥A′B.
(2)连接AA′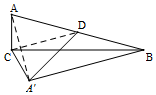
∵AD=A′D,∠ADA′=60°,
∴△ADA′是等边三角形.
∴AA′=AD=$\frac{1}{2}$AB,∠DAA′=60°.
∴∠AA′B=180°-∠A′AB-∠ABA′=90°.
∵AB=4,
∴AA′=2.
∴由勾股定理得:A′B2=AB2-AA′2=42-22=12.
点评 本题主要考查的是翻折的性质、勾股定理的应用、等边三角形的性质和判定、等腰三角形的性质,熟练掌握相关知识是解题的关键.


科目:初中数学 来源: 题型:选择题

| A. | 1015 | B. | 1010 | C. | 1012 | D. | 1018 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
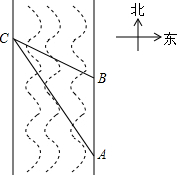 在一次数学活动课上,胡老师带领九(3)班的同学去测一条南北流向的河宽.如图所示,张一凡同学在河东岸点A出测到河对岸边有一点C,测得C在A的北偏西31°的方向上,沿河岸向北前进21m到达B处,测得C在B的北偏西45°的方向上. 请你根据以上的数据,帮助该同学计算出这条河的宽度.(tan31°=$\frac{3}{5}$)
在一次数学活动课上,胡老师带领九(3)班的同学去测一条南北流向的河宽.如图所示,张一凡同学在河东岸点A出测到河对岸边有一点C,测得C在A的北偏西31°的方向上,沿河岸向北前进21m到达B处,测得C在B的北偏西45°的方向上. 请你根据以上的数据,帮助该同学计算出这条河的宽度.(tan31°=$\frac{3}{5}$)查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com