
【题目】如图,在平行四边形ABCD中,对角线AC、BD相交于点O,BD=2AD,E、F、G分别是OC、OD、AB的中点,下列结论:①BE⊥AC;②四边形BEFG是平行四边形;③△EFG≌△GBE;④EG=EF,其中正确的个数是( )
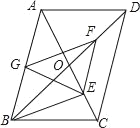
A.1B.2C.3D.4
【答案】D
【解析】
由平行四边形的性质可得AB=CD,AD=BC,BO=DO=![]() BD,AO=CO,AB∥CD,即可得BO=DO=AD=BC,由等腰三角形的性质可判断①,由中位线定理和直角三角形的性质可判断②④,由平行四边形的性质可判断③,即可求解.
BD,AO=CO,AB∥CD,即可得BO=DO=AD=BC,由等腰三角形的性质可判断①,由中位线定理和直角三角形的性质可判断②④,由平行四边形的性质可判断③,即可求解.
解:∵四边形ABCD是平行四边形
∴AB=CD,AD=BC,BO=DO=![]() BD,AO=CO,AB∥CD
BD,AO=CO,AB∥CD
∵BD=2AD
∴BO=DO=AD=BC,且点E是OC中点
∴BE⊥AC,
∴①正确
∵E、F、分别是OC、OD中点
∴EF∥DC,CD=2EF
∵G是AB中点,BE⊥AC
∴AB=2BG=2GE,且CD=AB,CD∥AB
∴BG=EF=GE,EF∥CD∥AB
∴四边形BGFE是平行四边形,
∴②④正确,
∵四边形BGFE是平行四边形,
∴BG=EF,GF=BE,且GE=GE
∴△BGE≌△FEG(SSS)
∴③正确
故选D.


 每课必练系列答案
每课必练系列答案科目:初中数学 来源: 题型:
【题目】某市A,B两个蔬菜基地得知四川C,D两个灾民安置点分别急需蔬菜240t和260t的消息后,决定调运蔬菜支援灾区,已知A蔬菜基地有蔬菜200t,B蔬菜基地有蔬菜300t,现将这些蔬菜全部调运C,D两个灾区安置点.从A地运往C,D两处的费用分别为每吨20元和25元,从B地运往C,D两处的费用分别为每吨15元和18元.设从B地运往C处的蔬菜为x吨.
(1)请填写下表,并求两个蔬菜基地调运蔬菜的运费相等时x的值;
C | D | 总计/t | |
A | 200 | ||
B | x | 300 | |
总计/t | 240 | 260 | 500 |
(2)设A,B两个蔬菜基地的总运费为w元,求出w与x之间的函数关系式,并求
总运费最小的调运方案;
(3)经过抢修,从B地到C处的路况得到进一步改善,缩短了运输时间,运费每吨减少m元(m>0),其余线路的运费不变,试讨论总运费最小的调动方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD是△ABC的角平分线,过点D作DE∥BC交AB于点E,DF∥AB交BC于点F.
(1)求证:四边形BEDF为菱形;
(2)如果∠A=90°,∠C=30°,BD=12,求菱形BEDF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某校落实新课改精神的情况,现以该校九年级二班的同学参加课外活动的情况为样本,对其参加“球类”、“绘画类”、“舞蹈类”、“音乐类”、“棋类”活动的情况进行调查统计,并绘制了如图所示的统计图.
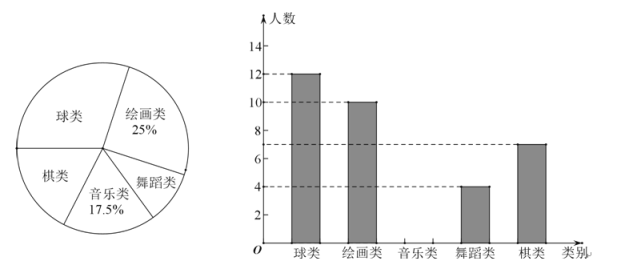
(1)参加音乐类活动的学生人数为 人,参加球类活动的人数的百分比为 ;
(2)该校学生共600人,则参加棋类活动的人数约为 ;
(3)该班参加舞蹈类活动的四位同学中,有一位男生(用E表示)和3位女生(分别用F,G,H表示),先准备从中选取两名同学组成舞伴,请用列表或画树状图得方法求恰好选中一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知抛物线y=ax2+bx+3=0(a≠0)与x轴交于点A(1,0)和点B(﹣3,0),与y轴交于点C
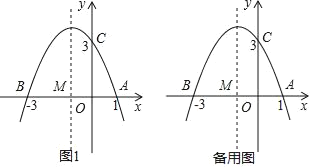
(1)求抛物线的解析式;
(2)设抛物线的对称轴与x轴交于点M,请问在对称轴上是否存在点P,使△CMP为等腰三角形?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由;
(3)在抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
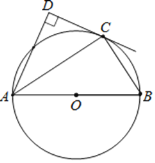
【题目】如图,点C在以AB为直径的⊙O上,AD与过点C的切线垂直,垂足为点D.
(1)求证:AC平分∠DAB;
(2)求证:AC2=ADAB;
(3)若AD=![]() ,sinB=
,sinB=![]() ,求线段BC的长.
,求线段BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校九年级学生的理化实验操作情况,随机抽查了40名同学实验操作的得分.根据获取的样本数据,制作了如下的条形统计图和扇形统计图.请根据相关信息,解答下列问题:

(Ⅰ)扇形 ①的圆心角的大小是 ;
(Ⅱ)求这40个样本数据的平均数、众数、中位数;
(Ⅲ)若该校九年级共有320名学生,估计该校理化实验操作得满分(10分)有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解学生在假期中的课外阅读情况,七(1)班针对“你最喜爱的课外阅读书目“进行调查(每名学生必须选一类且只能选一类阅读书目),并根据调查结果列出统计表,绘制成扇形统计图.
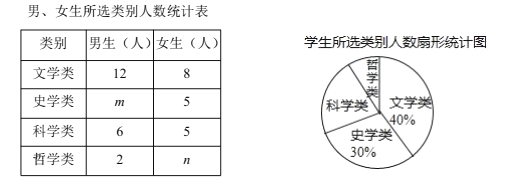
(1)m=__________,n=__________;
(2)扇形统计图中“科学类”所对应扇形圆心角度数为__________°;
(3)从选哲学类的学生中,随机选取两名学生参加学校团委组织的辩论赛,请用树状图或列表法求出所选取的两名学生都是男生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com