
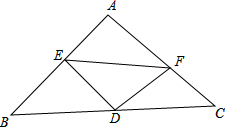
 如图,Rt△ABC中,∠A=90°,AB=AC=2,点D是BC边的中点,点E是AB边上的一个动点(不与A、B重合),DF⊥DE交AC于F.设BE=x,FC=y.
如图,Rt△ABC中,∠A=90°,AB=AC=2,点D是BC边的中点,点E是AB边上的一个动点(不与A、B重合),DF⊥DE交AC于F.设BE=x,FC=y.分析 (1)过D作DH⊥AB交AB于H,DN⊥AC交AC于N.根据三角形中位线的性质可得DH=DN,根据余角的性质可得∠EDH=∠FDN,根据ASA可证△EDH≌△FDN,根据全等三角形的性质即可证明DE=DF;
(2)根据全等三角形的性质可得HE=NF,从而得到y关于x的函数关系式,以及x的定义域;
(3)连接HN,根据三角形中位线的性质可得x为1时,EF∥BC.
解答 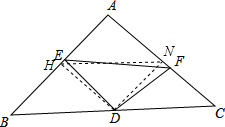 解:(1)过D作DH⊥AB交AB于H,DN⊥AC交AC于N.
解:(1)过D作DH⊥AB交AB于H,DN⊥AC交AC于N.
∵∠A=90°,点D是BC边的中点,
∴DN∥AB,DN=$\frac{1}{2}$AB,DH∥AC,DH=$\frac{1}{2}$AC,
∵AB=AC=2,
∴DH=DN=1,
∴∠NDH=90°,
∵∠NDF+∠NDE=90°,∠NDE+EDH=90°,
∴∠EDH=∠FDN,
在△EDH与△FDN中,
$\left\{\begin{array}{l}{∠EDH=∠FDN}\\{DH=DN}\\{∠EHD=∠FND}\end{array}\right.$,
∴△EDH≌△FDN(ASA),
∴DE=DF;
(2)∵△EDH≌△FDN,
∴HE=NF,
∴x-$\frac{1}{2}$AB=$\frac{1}{2}$AC-y,即y=2-x,
∵E是AB边上的一个动点(不与A、B重合),
∴0<x<2;
(3)连接HN,当E与H重合时,EF∥BC,
∵此时x=BH=1,
∴当x=1时,EF∥BC.
点评 本题考查了全等三角形的判定与性质,三角形中位线的性质,正确证明△EDH≌△FDN是关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 印制x(张) | … | 100 | 200 | 300 | … |
| 收费y(元) | … | 1 | 30 | 45 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
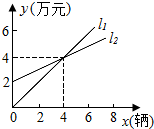 如图,l1表示信达商场一天的某型电脑销售额与销售量的关系,l2表示该商场一天的销售成本与电脑销售量的关系,观察图象,解决以下问题:
如图,l1表示信达商场一天的某型电脑销售额与销售量的关系,l2表示该商场一天的销售成本与电脑销售量的关系,观察图象,解决以下问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
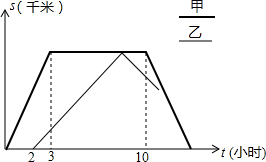 甲乙两车从姜堰去往扬州市,甲比乙早出发了2个小时,甲到达扬州市后停留一段时间返回,乙到达扬州市后立即返回.甲车往返的速度都为80千米/时,乙车往返的速度都为40千米/时,下图是两车距姜堰的路程S(千米)与行驶时间t(小时)之间的函数图象.请结合图象回答下列问题:
甲乙两车从姜堰去往扬州市,甲比乙早出发了2个小时,甲到达扬州市后停留一段时间返回,乙到达扬州市后立即返回.甲车往返的速度都为80千米/时,乙车往返的速度都为40千米/时,下图是两车距姜堰的路程S(千米)与行驶时间t(小时)之间的函数图象.请结合图象回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com