【题目】如图所示，数轴被折成90°，圆的周长为4个单位长度，在圆的4等分点处标上数字0，1，2，3，先让圆周上数字2所对应的点与数轴上的数3所对应的点重合，数轴固定，圆紧贴数轴沿着数轴的正方向滚动，那么数轴上的数2018将与圆周上的数字________重合．
英才点津系列答案
红果子三级测试卷系列答案科目：初中数学 来源： 题型：
【题目】如图，一个四边形花坛ABCD，被两条线段MN,EF分成四个部分，分别种上红、黄、紫、白四种花卉，种植面积依次是S1,S2,S3,S4，若MN∥AB∥CD，EF∥DA∥CB，则有（ ）
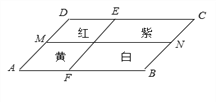
A. S1=S4 B. S1+S4=S2+S3 C. S1S4=S2S3 D. 都不对
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，水坝的横断面是梯形，背水坡AB的坡角∠BAD=60°，坡长AB=20 
m，为加强水坝强度，降坝底从A处后水平延伸到F处，使新的背水坡角∠F=45°，求AF的长度（结果精确到1米，参考数据： 
1.414， ≈1.732）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】解方程
（1）x2＝49
（2）3x2－7x＝0
（3）
（直接开平方法）
（4）
（用配方法）
（5）
（因式分解法）
（6）
（7）（x－2）（x－5）=－2
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知抛物线与x交于A（﹣1，0）、E（3，0）两点，与y轴交于点B（0，3）．
（1）求抛物线的解析式；
（2）设抛物线顶点为D，求四边形AEDB的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图，在△ABC中，∠C=90°，AE是△ABC的角平分线；ED平分∠AEB，交AB于点D；∠CAE∠B．
（1）求∠B的度数．
（2）如果AC=3cm，求AB的长度．
（3）猜想：ED与AB的位置关系，并证明你的猜想．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读理解，完成下列各题
定义：已知A、B、C 为数轴上任意三点，若点C 到A 的距离是它到点B 的距离的2 倍，则称点C 是[A，B]的2 倍点．例如：如图1，点C 是[A，B]的2 倍点，点D 不是[A，B]的2 倍点，但点D 是[B，A]的2 倍点，根据这个定义解决下面问题：
（1）在图1 中，点A 是 的2倍点，点B是 的2 倍点；（选用A、B、C、D 表示，不能添加其他字母）；
（2）如图2，M、N 为数轴上两点，点M 表示的数是﹣2，点N 表示的数是4，若点E是[M，N]的2倍点，则点E 表示的数是 ；
（3）若P、Q 为数轴上两点，点P在点Q的左侧，且PQ=m，一动点H从点Q 出发，以每秒2个单位长度的速度沿数轴向左运动，设运动时间为t 秒，求当t 为何值时，点H 恰好是P和Q两点的2倍点？（用含m 的代数式表示）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
