
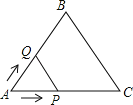
【题目】如图,等边△ABC的边长为2cm,点P从点A出发,以1cm/s的速度沿AC向点C运动,到达点C停止;同时点Q从点A出发,以2cm/s的速度沿AB﹣BC向点C运动,到达点C停止,设△APQ的面积为y(cm2),运动时间为x(s),则下列最能反映y与x之间函数关系的图象是( )
A.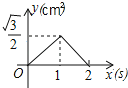 B.
B.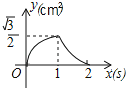
C.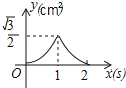 D.
D.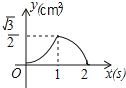
【答案】D
【解析】
根据点Q的位置分两种情况讨论,当点Q在AB上运动时,求得y与x之间函数解析式,当点Q在BC上运动时,求得y与x之间函数解析式,最后根据分段函数的图象进行判断即可.
解:由题得,点Q移动的路程为2x,点P移动的路程为x,
∠A=∠C=60°,AB=BC=2,
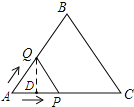
①如图,当点Q在AB上运动时,过点Q作QD⊥AC于D,则
AQ=2x,DQ=![]() x,AP=x,
x,AP=x,
∴△APQ的面积y=![]() ×x×
×x×![]() x=
x=![]() (0<x≤1),
(0<x≤1),
即当0<x≤1时,函数图象为开口向上的抛物线的一部分,故(A)、(B)排除;
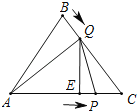
②如图,当点Q在BC上运动时,过点Q作QE⊥AC于E,则
CQ=4﹣2x,EQ=2![]() ﹣
﹣![]() x,AP=x,
x,AP=x,
∴△APQ的面积y=![]() ×x×(2
×x×(2![]() ﹣
﹣![]() x)=﹣
x)=﹣![]() +
+![]() x(1<x≤2),
x(1<x≤2),
即当1<x≤2时,函数图象为开口向下的抛物线的一部分,故(C)排除,而(D)正确;
故选:D.


科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径, BC交⊙O于点D,E是![]() 的中点,连接AE交BC于点F,∠ACB =2∠EAB.
的中点,连接AE交BC于点F,∠ACB =2∠EAB.
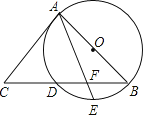
(1)求证:AC是⊙O的切线;
(2)若![]() ,
,![]() ,求BF的长.
,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
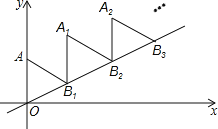
【题目】如图,放置的△OAB1,△B1A1B2,△B2A2B3,都是边长为2的等边三角形,边AO在Y轴上,点B1、B2、B3都在直线y=![]() x上,则点A2019的坐标为__________________
x上,则点A2019的坐标为__________________
查看答案和解析>>
科目:初中数学 来源: 题型:
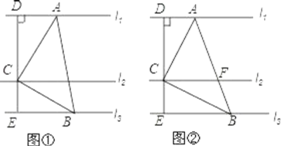
【题目】探究:如图①,直线l1∥l2∥l3,点C在l2上,以点C为直角顶点作∠ACB=90°,角的两边分别交l1与l3于点A、B,连结AB,过点C作CD⊥l1于点D,延长DC交l3于点E.
(1)求证:△ACD∽△CBE.
(2)应用:如图②,在图①的基础上,设AB与l2的交点为F,若AC=BC,l1与l2之间的距离为2,l2与l3之间的距离为1,则AF的长度是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,BC>AB,在BC边上取点D,使AB=BD,构造正方形ABDE,DE交AC于点F,作EG⊥AC交AC于点G,交BC于点H.
(1)求证:EF=DH;
(2)若AB=6,DH=2DF,求AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店老板到厂家选购![]() 、
、![]() 两种品牌的羽绒服,
两种品牌的羽绒服,![]() 品牌羽绒服每件进价比
品牌羽绒服每件进价比![]() 品牌羽绒服每件进价多
品牌羽绒服每件进价多![]() 元,若用
元,若用![]() 元购进
元购进![]() 种羽绒服的数量是用
种羽绒服的数量是用![]() 元购进
元购进![]() 种羽绒服数量的
种羽绒服数量的![]() 倍.
倍.
(1)求![]() 、
、![]() 两种品牌羽绒服每件进价分别为多少元?
两种品牌羽绒服每件进价分别为多少元?
(2)若![]() 品牌羽绒服每件售价为
品牌羽绒服每件售价为![]() 元,
元,![]() 品牌羽绒服每件售价为
品牌羽绒服每件售价为![]() 元,服装店老板决定一次性购进
元,服装店老板决定一次性购进![]() 、
、![]() 两种品牌羽绒服共
两种品牌羽绒服共![]() 件,在这批羽绒服全部出售后所获利润不低于
件,在这批羽绒服全部出售后所获利润不低于![]() 元,则最少购进
元,则最少购进![]() 品牌羽绒服多少件?
品牌羽绒服多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在 10×6 的正方形网格中,每个小正方形的边长均为 1,线段 AB 的端点 A、B 均在小正方形的顶点上.
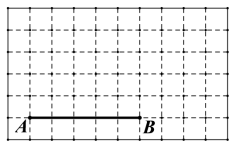
(1)在图中画出以 AB 为一腰的等腰△ABC,点 C 在小正方形顶点上,△ABC 为钝角三角形,且△ABC 的面积为![]() ;
;
(2)在图中画出以 AB 为斜边的直角三角形 ABD, 点 D在小正方形的顶点上,且 AD>BD;
(3)连接 CD,请你直接写出线段 CD 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
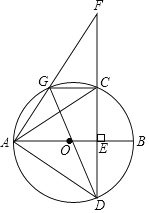
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点E,G是![]() 上一动点,AG,DC的延长线交于点F,连接AC,AD,GC,GD.
上一动点,AG,DC的延长线交于点F,连接AC,AD,GC,GD.
(1)求证:∠FGC=∠AGD;
(2)若AD=6.
①当AC⊥DG,CG=2时,求sin∠ADG;
②当四边形ADCG面积最大时,求CF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com