
分析 首先计算乘方、开方,然后计算乘法,最后从左向右依次计算,求出算式的值是多少即可.
解答 解:cos45°•(-$\frac{1}{2}$)-2?-(2$\sqrt{2}$-$\sqrt{3}$)0+|4-$\sqrt{18}$|+$\frac{1}{\sqrt{2}}$
=$\frac{\sqrt{2}}{2}$×4-1+3$\sqrt{2}$-4+$\frac{\sqrt{2}}{2}$
=$\frac{11\sqrt{2}}{2}$-5
点评 此题主要考查了实数的运算,要熟练掌握,解答此题的关键是要明确:在进行实数运算时,和有理数运算一样,要从高级到低级,即先算乘方、开方,再算乘除,最后算加减,有括号的要先算括号里面的,同级运算要按照从左到右的顺序进行.另外,有理数的运算律在实数范围内仍然适用.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
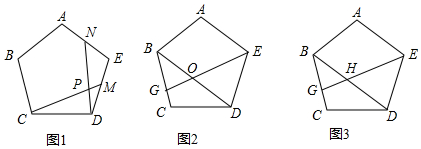
 如图,在菱形ABCD中,AB=6,∠DAB=60°,AE分别交BC、BD于点E、F,若CE=2,连接CF.以下结论:①∠BAF=∠BCF;②点E到AB的距离是2$\sqrt{3}$;③S△CDF:S△BEF=9:4;④tan∠DCF=$\frac{3}{7}$.其中正确的有( )
如图,在菱形ABCD中,AB=6,∠DAB=60°,AE分别交BC、BD于点E、F,若CE=2,连接CF.以下结论:①∠BAF=∠BCF;②点E到AB的距离是2$\sqrt{3}$;③S△CDF:S△BEF=9:4;④tan∠DCF=$\frac{3}{7}$.其中正确的有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
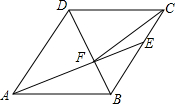
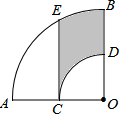 如图,在扇形AOB中,∠AOB=90°,点C为OA的中点,CE⊥OA交弧AB于点E,以点O为圆心,OC的长为半径作弧CD交OB于点D,若OA=4,则阴影部分的面积为$\frac{1}{3}$π+2$\sqrt{3}$.
如图,在扇形AOB中,∠AOB=90°,点C为OA的中点,CE⊥OA交弧AB于点E,以点O为圆心,OC的长为半径作弧CD交OB于点D,若OA=4,则阴影部分的面积为$\frac{1}{3}$π+2$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
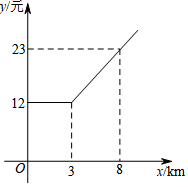 为了追求更舒适的出行体验,利用网络呼出专车的打车方式受到大众欢迎.据了解在非高峰期时,某种专车所收取的费用y(元)与行驶里程x(km)的函数关系如图所示,请根据图象解答下列问题:
为了追求更舒适的出行体验,利用网络呼出专车的打车方式受到大众欢迎.据了解在非高峰期时,某种专车所收取的费用y(元)与行驶里程x(km)的函数关系如图所示,请根据图象解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com