
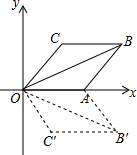
 如图,菱形OABC的一边OA在x轴上,将菱形OABC沿x轴翻折到四边形OAB′C′的位置,若OB=2$\sqrt{3}$,∠C=120°,则点B′的坐标为(3,$-\sqrt{3}$).
如图,菱形OABC的一边OA在x轴上,将菱形OABC沿x轴翻折到四边形OAB′C′的位置,若OB=2$\sqrt{3}$,∠C=120°,则点B′的坐标为(3,$-\sqrt{3}$). 分析 由∠C=120°可求得∠COA=60°,由菱形的性质可知:∠BOA=30°,由OB=2$\sqrt{3}$,从可求得点B的横纵坐标,最后根据关于x轴对称点的坐标特点可知求得点B′的坐标.
解答 解:∵四边形OABC是菱形,
∴∠C+∠COA=180°,
∴∠COA=180°-120°=60°.
由菱形的性质可知:∠BOA=30°,
∴点B的横坐标=OB•cos30°=2$\sqrt{3}×\frac{\sqrt{3}}{2}$=3,点B的纵坐标=OB•sin30°=2$\sqrt{3}×\frac{1}{2}$=$\sqrt{3}$.
由关于x轴对称点的坐标特点可知:点B′(3,$-\sqrt{3}$).
故答案为:(3,$-\sqrt{3}$).
点评 本题主要考查的是菱形的性质、翻折变换和特殊锐角三角函数值,根据菱形的性质求得∠BOA=30°是解题的关键.


科目:初中数学 来源: 题型:填空题
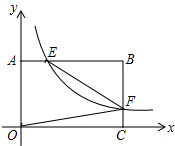 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象与矩形OABC的边AB、BC分别交于点E、F,若S矩形OABC=2,则当k=1时,四边形OAEF的面积最大.
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象与矩形OABC的边AB、BC分别交于点E、F,若S矩形OABC=2,则当k=1时,四边形OAEF的面积最大.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
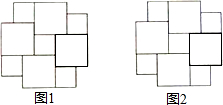 如图是以两个大小不同的正方形为基本图案镶嵌而成的图形,请仅用无刻度的直尺按不同的方法分别在图1、图2中画一个正方形,使它的面积等于这两个大小不同的正方形的面积之和.要求:(1)用虚线连线;(2)要标注你所画正方形的顶点字母.
如图是以两个大小不同的正方形为基本图案镶嵌而成的图形,请仅用无刻度的直尺按不同的方法分别在图1、图2中画一个正方形,使它的面积等于这两个大小不同的正方形的面积之和.要求:(1)用虚线连线;(2)要标注你所画正方形的顶点字母.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 类别 | 进价(元/台) | 洗衣机 |
| 进价(元/台) | 1800 | 1500 |
| 售价(元/台) | 2000 | 1600 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com