练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    20．若不等式组$\left\{\begin{array}{l}{x≤m}\\{x＞1}\end{array}\right.$有解，则m的取值范围为（　　）
    A．m＞1B．m≥1C．m＜1D．m≤1

    分析 根据不等式组有解的口诀解答即可．

    解答 解：∵不等式组$\left\{\begin{array}{l}{x≤m}\\{x＞1}\end{array}\right.$有解，
    ∴m的取值范围为m＞1．
    故选A．

    点评 本题主要考查了一元一次不等式组解集的求法，其简便求法就是用口诀求解．求不等式组解集的口诀：同大取大，同小取小，大小小大中间找，大大小小找不到（无解）．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    10．甲同学说：（1）班与（5）班得分比为6：5；乙同学说：（1）班得分比（5）班得分的2倍少40分．若设（1）班得x分，（5）班得y分，根据题意所列的方程组应为（　　）
    A．$\left\{\begin{array}{l}6x=5y\\ x=2y-40\end{array}\right.$B．$\left\{\begin{array}{l}6x=5y\\ x=2y+40\end{array}\right.$C．$\left\{\begin{array}{l}5x=6y\\ x=2y+40\end{array}\right.$D．$\left\{\begin{array}{l}5x=6y\\ x=2y-40\end{array}\right.$

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    11．（1-$\frac{1}{{2}^{2}}$）（1-$\frac{1}{{3}^{2}}$）（1-$\frac{1}{{4}^{2}}$）（1-$\frac{1}{{5}^{2}}$）（1-$\frac{1}{{6}^{2}}$）（1-$\frac{1}{{7}^{2}}$）（1-$\frac{1}{{8}^{2}}$）=$\frac{9}{16}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．在△ABC中，AB=AC，AD⊥BC于点D，DE∥AB交AC于点E，若∠ADE=25°，则∠BAC的度数为50°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．如图，抛物线y=-x2+bx+c与x轴交于A、B两点，与y轴交与点C，点O为坐标原点，点D为抛物线的顶点，点E在抛物线上，点F在x轴上，四边形OCEF为矩形，且OF=2，EF=3
    （1）求抛物线的解析式并配成顶点式（要求写出过程）；
    （2）求△ABD的面积；
    （3）将△AOC绕点C逆时针旋转90°，点A对应点为点G，问点G是否在该抛物线上？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．若数a使关于x的不等式组$\left\{\begin{array}{l}{\frac{a+x}{2}≥x-2}\\{\frac{x}{3}-（x-2）＞\frac{2}{3}}\end{array}\right.$的解为x＜2，且使关于x的分式方程$\frac{x-1}{4-x}$+$\frac{a+5}{x-4}$=-4有正整数解，则满足条件的a的值之和为（　　）
    A．12B．11C．10D．9

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

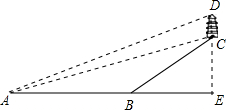    12．鹅岭公园是重庆最早的私家园林，前身为礼园，是国家级AAA旅游景区，园内有一瞰胜楼，登上高楼能欣赏到重庆的优美景色，周末小嘉同学游览鹅岭公园，如图，在A点处观察到毗胜楼楼底C的仰角为12°，楼顶D的仰角为13°，BC是一斜坡，测得点B与CD之间的水平距离BE=450米．BC的坡度i=8：15，则测得水平距离AE=1200m，BC的坡度i=8：15，则瞰胜楼的高度CD为（　　）米．（参考数据：tan12°=0.2，tan13°=0.23）
    A．34B．35C．36D．37

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．已知：抛物线有=-x2+bx+c经过A（-1，0）、B（5，0）两点，顶点为P．求：
    （Ⅰ）求b，c的值；
    （Ⅱ）求△ABP的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．如图（1），在矩形ABCD中，AB=3，BC=4，连接BD．现将一个足够大的直角三角板的直角顶点P放在BD所在的直线上，一条直角边过点C，另一条直角边与AB所在的直线交于点G．
    （1）是否存在这样的点P，使点P、C、G为顶点的三角形与△GCB全等？若存在，画出图形，并直接在图形下方写出BG的长．（如果你有多种情况，请用①、②、③、…表示，每种情况用一个图形单独表示，如果图形不够用，请自己画图）
    （2）如图（2），当点P在BD的延长线上时，以P为圆心、PB为半径作圆分别交BA、BC延长线于点E、F，连EF，分别过点G、C作GM⊥EF，CN⊥EF，M、N为垂足．试探究PM与FN的关系．

    查看答案和解析>>

    同步练习册答案