
【题目】如图1,已知平行四边形ABCD顶点A的坐标为(2,6),点B在y轴上,且AD∥BC∥x轴,过B,C,D三点的抛物线y=ax2+bx+c(a≠0)的顶点坐标为(2,2),点F(m,6)是线段AD上一动点,直线OF交BC于点E.
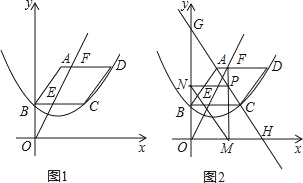
(1)求抛物线的表达式;
(2)设四边形ABEF的面积为S,请求出S与m的函数关系式,并写出自变量m的取值范围;
(3)如图2,过点F作FM⊥x轴,垂足为M,交直线AC于P,过点P作PN⊥y轴,垂足为N,连接MN,直线AC分别交x轴,y轴于点H,G,试求线段MN的最小值,并直接写出此时m的值.
【答案】(1)抛物线解析式为y=![]() x2﹣x+3;(2)S=
x2﹣x+3;(2)S=![]() m﹣3(2<m≤6);(3)当m=
m﹣3(2<m≤6);(3)当m=![]() 时,MN最小=
时,MN最小=![]() .
.
【解析】试题分析:(1)根据平行四边形的性质和抛物线的特点确定出点D,然而用待定系数法确定出抛物线的解析式.(2)根据AD∥BC∥x轴,且AD,BC间的距离为3,BC,x轴的距离也为3,F(m,6),确定出E(![]() ,3),从而求出梯形的面积.(3)先求出直线AC解析式,然后根据FM⊥x轴,表示出点P(m,﹣
,3),从而求出梯形的面积.(3)先求出直线AC解析式,然后根据FM⊥x轴,表示出点P(m,﹣![]() m+9),最后根据勾股定理求出MN=
m+9),最后根据勾股定理求出MN=![]() ,从而确定出MN最大值和m的值.
,从而确定出MN最大值和m的值.
试题解析:(1)∵过B,C,D三点的抛物线y=ax2+bx+c(a≠0)的顶点坐标为(2,2),
∴点C的横坐标为4,BC=4,
∵四边形ABCD为平行四边形,
∴AD=BC=4,
∵A(2,6),
∴D(6,6),
设抛物线解析式为y=a(x﹣2)2+2,
∵点D在此抛物线上,
∴6=a(6﹣2)2+2,
∴a=![]() ,
,
∴抛物线解析式为y=![]() (x﹣2)2+2=
(x﹣2)2+2=![]() x2﹣x+3,
x2﹣x+3,
(2)∵AD∥BC∥x轴,且AD,BC间的距离为3,BC,x轴的距离也为3,F(m,6)
∴E(![]() ,3),
,3),
∴BE=![]() ,
,
∴S=![]() (AF+BE)×3=
(AF+BE)×3=![]() (m﹣2+
(m﹣2+![]() )×3=
)×3=![]() m﹣3
m﹣3
∵点F(m,6)是线段AD上,
∴2≤m≤6,
即:S=![]() m﹣3(2≤m≤6).
m﹣3(2≤m≤6).
(3)∵抛物线解析式为y=![]() x2﹣x+3,
x2﹣x+3,
∴B(0,3),C(4,3),
∵A(2,6),
∴直线AC解析式为y=﹣![]() x+9,
x+9,
∵FM⊥x轴,垂足为M,交直线AC于P
∴P(m,﹣![]() m+9),(2≤m≤6)
m+9),(2≤m≤6)
∴PN=m,PM=﹣![]() m+9,
m+9,
∵FM⊥x轴,垂足为M,交直线AC于P,过点P作PN⊥y轴,
∴∠MPN=90°,
∴MN=![]() =
=![]() =
=![]()
∵2≤m≤6,
∴当m=![]() 时,MN最小=
时,MN最小=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】一天,小明在玩纸片拼图游戏时,发现利用图①中的三种材料各若干,可以拼出一些长方形来解释某些等式,比如图②可以解释为等式:![]() .
.

(1)则图③可以解释为等式: .
(2)在虚线框中用图①中的基本图形若干块(每种至少用一次)拼成一个长方形,使拼出的长方形面积为![]() ,并请在图中标出这个长方形的长和宽.
,并请在图中标出这个长方形的长和宽.
(3)如图④,大正方形的边长为![]() ,小正方形的边长为
,小正方形的边长为![]() ,若用
,若用![]() 、
、![]() 表示四个长方形的两边长(
表示四个长方形的两边长(![]() ),观察图案,指出以下关系式:(
),观察图案,指出以下关系式:(![]() )
)![]() ;(
;(![]() )
)![]() ;(
;(![]() )
)![]() ; (
; (![]() )
)![]() .其中正确的关系式的个数有 个.
.其中正确的关系式的个数有 个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90,AC=6,BC=8,动点P从点A开始,沿边AC向点C以每秒1个单位长度的速度运动,动点D从点A开始,沿边AB向点B以每秒![]() 个单位长度的速度运动,且恰好能始终保持连结两动点的直线PD⊥AC,动点Q从点C开始,沿边CB向点B以每秒2个单位长度的速度运动,连结PQ.点P,D,Q分别从点A,C同时出发,当其中一点到达端点时,另两个点也随之停止运动,设运动时间为t秒(t≥0).
个单位长度的速度运动,且恰好能始终保持连结两动点的直线PD⊥AC,动点Q从点C开始,沿边CB向点B以每秒2个单位长度的速度运动,连结PQ.点P,D,Q分别从点A,C同时出发,当其中一点到达端点时,另两个点也随之停止运动,设运动时间为t秒(t≥0).
(1)当t为何值时,四边形BQPD的面积为△ABC面积的![]() ?
?
(2)是否存在t的值,使四边形PDBQ为平行四边形?若存在,求出t的值;若不存在,说明理由;
(3)是否存在t的值,使四边形PDBQ为菱形?若存在,求出t的值;若不存在,说明理由,并探究如何改变点Q的速度(匀速运动),使四边形PDBQ在某一时刻为菱形,求点Q的速度。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了选拔学生参加“汉字听写大赛”,对九年级一班、二班各10名学生进行汉字听写测试.计分采用10分制(得分均取整数),成绩达到6分或6分以上为及格,得到9分为优秀,成绩如表1所示,并制作了成绩分析表(表2).
表1
一班 | 5 | 8 | 8 | 9 | 8 | 10 | 10 | 8 | 5 | 5 |
二班 | 10 | 6 | 6 | 9 | 10 | 4 | 5 | 7 | 10 | 8 |
表2
班级 | 平均数 | 中位数 | 众数 | 方差 | 及格率 | 优秀率 |
一班 | 7.6 | 8 | 3.82 | 70% | 30% | |
二班 | b | 7.5 | 10 | 4.94 | 80% | 40% |
(1)在表2中,a= ,b= ;
(2)有人说二班的及格率、优秀率均高于一班,所以二班比一班好;但也有人认为一班成绩比二班好,请你给出坚持一班成绩好的两条理由;
(3)一班、二班获满分的中同学性别分别是1男1女、2男1女,现从这两班获满分的同学中各抽1名同学参加“汉字听写大赛”,用树状图或列表法求出恰好抽到1男1女两位同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E是正方形ABCD的边AB上的动点,但始终保持EF⊥DE交BC于点F.
(1)求证:△ADE∽△BEF;
(2)若正方形的边长为4,设AE=x,BF=y,求y与x之间的函数解析式;
(3)当x取何值时,y有最大值?并求出这个最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABDE、CDFI、EFGH的面积分别为25、9、16,△AEH、△BDC、△GFI的面积分别为S1、S2、S3,则S1+S2+S3=_____.
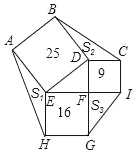
查看答案和解析>>
科目:初中数学 来源: 题型:
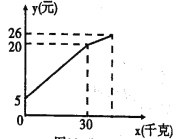
【题目】一农民带了若干千克自产的萝卜进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售.售出萝卜千克数与他手中持有的钱数(含备用零钱)的关系如图所示,结合图象回答下列问题:
(1)降价前他每千克萝卜出售的价格是多少?
(2)降价后他按每千克0.4元将剩余萝卜售完,这时他手中的钱(含备用零钱)是26元,问他一共带了多少千克萝卜?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市举行“第十七届中小学生书法大赛”作品比赛,已知每幅参赛作品成绩记为![]() ,组委会从1000幅书法作品中随机抽取了部分参赛作品,统计了它们的成绩,并绘制成如下统计图表.
,组委会从1000幅书法作品中随机抽取了部分参赛作品,统计了它们的成绩,并绘制成如下统计图表.
分数段 | 频数 | 百分比 |
| 38 | 0.38 |
| ________ | 0.32 |
| ________ | ________ |
| 10 | 0.1 |
合计 | ________ | 1 |

根据上述信息,解答下列问题:
(1)这次书法作品比赛成绩的调查是采用_____(填“普查”或“抽样调查”),样本是_____.
(2)完成上表,并补全书法作品比赛成绩频数直方图.
(3)若80分(含80分)以上的书法作品将被评为等级奖,试估计全市获得等级奖的数量.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com