
【题目】解方程:
(1)(x―1)2=4
(2)x2-3x-2=0
(3)x2+6x=7
(4)2(x2-x)-(x-1)(x+3)+1=0
【答案】(1)x1=3,x2=-1;(2)x1=![]() ;x2=
;x2=![]() ;(3)x1=1,x2=-7;(4)x1=x2=2.
;(3)x1=1,x2=-7;(4)x1=x2=2.
【解析】
(1)用直接开平方法求解即可;
(2)用公式法求解即可;
(3)移项后用因式分解法求解即可;
(4)整理后用因式分解法求解即可.
(1)∵(x―1)2=4 ,
∴x-1=±2,
∴)x1=3,x2=-1;
(2)x2-3x-2=0,
∵=9+8=17>0,
∴x=![]() ,
,
∴x1=![]() ;x2=
;x2=![]() ;
;
(3)∵x2+6x=7,
∴x2+6x-7=0,
∴(x-1)(x-7)=0,
∴x1=1,x2=-7;
(4)2(x2-x)-(x-1)(x+3)+1=0,
整理得
x2-4x+4=0,
∴(x-2)2=0,
x1=x2=2.


科目:初中数学 来源: 题型:
【题目】如图所示,二次函数y=ax2+bx+c(a≠0)的图象经过点(﹣1,2),且与x轴交点的横坐标为x1、x2,其中﹣2<x1<﹣1、0<x2<1下列结论:①4a﹣2b+c<0②2a﹣b<0③abc>0④b2+8a>4ac正确的结论是_____.
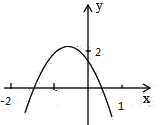
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件![]() 元,现在的售价为每件
元,现在的售价为每件![]() 元,每星期可卖出
元,每星期可卖出![]() 件.市场调查反映:如果每件的售价每涨
件.市场调查反映:如果每件的售价每涨![]() 元(售价每件不能高于
元(售价每件不能高于![]() 元),那么每星期将少卖出
元),那么每星期将少卖出![]() 件.设每件涨价
件.设每件涨价![]() 元(
元(![]() 为非负整数),每星期的销量为
为非负整数),每星期的销量为![]() 件.
件.
①求![]() 与
与![]() 的函数关系式及自变量
的函数关系式及自变量![]() 的取值范围;
的取值范围;
②如何定价才能使每星期的利润最大?每星期的最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
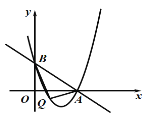
【题目】如图,在平面直角坐标系![]() 中,直线
中,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,抛物线经过
,抛物线经过![]() 、
、![]() 两点,且对称轴为直线
两点,且对称轴为直线![]() .
.
(1)求抛物线的表达式;
(2)如果点![]() 是这抛物线上位于
是这抛物线上位于![]() 轴下方的一点,且△
轴下方的一点,且△![]() 的面积是
的面积是![]() .求点
.求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义符号min{a,b}的含义为:当a≥b时,min{a,b}=b;当a<b时,min{a,b}=a,如:min{1,-2)=-2,min{-3,-2)=-3,则方程min{x,-x}=x2-1的解是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线的顶点坐标为(2,1),且经过点(-1,-8).
(1)求此抛物线的函数表达式;
(2)求抛物线与坐标轴的交点坐标;
(3)若自变量x的取值范围是![]() ,求对应的函数值y的取值范围.
,求对应的函数值y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 是原点,
是原点,![]() 两点的坐标分别为
两点的坐标分别为![]() ,
,![]() .
.
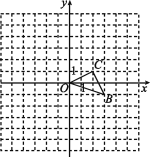
(1)以点![]() 为位似中心,在
为位似中心,在![]() 轴的左侧将
轴的左侧将![]() 扩大为原来的两倍(即新图与原图的相似比为
扩大为原来的两倍(即新图与原图的相似比为![]() ),画出图形,并写出点
),画出图形,并写出点![]() 的对应点的坐标;
的对应点的坐标;
(2)如果![]() 内部一点
内部一点![]() 的坐标为
的坐标为![]() ,写出点
,写出点![]() 的对应点
的对应点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com