
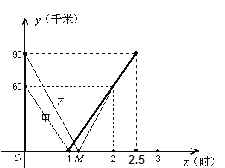
【题目】(本题满分10分)如图①,一条笔直的公路上有A、B、C三地,B.C两地相距150千米,甲、乙两辆汽车分别从B、C两地同时出发,沿公路匀速相向而行,分别驶往C、B两地.甲、乙两车到A地的距离y1、y2(千米)与行驶时间x(时)的关系如图②所示.根据图像进行以下探究:

(1)请在图①中标出A地的位置,并作简要的文字说明;
(2)求图②中M点的坐标,并解释该点的实际意义;
(3)在图②中补全甲车的函数图像,求甲车到A地的距离y1与行驶时间x的函数表达式;
(4)A地设有指挥中心,指挥中心及两车都配有对讲机,两部对讲机在15千米之内(含15千米)时能够互相通话,求两车可以同时与指挥中心用对讲机通话的时间.
【答案】(1)A地位置如图所示.使点A满足AB:AC=2:3;
(2)M(1.2,0),点M表示乙车1.2小时到达A地;
(3)作图见试题解析,![]() ;
;
(4)![]() 小时.
小时.
【解析】
试题(1)先根据题意作出图形,根据图形的特征即可得到结果;
(2)先根据题意求得乙车的速度,再求出M点对应的时间,即可得到结果;;
(3)根据待定系数法即可求得结果;
(4)根据“两部对讲机在15千米之内(含15千米)时能够互相通话”作为不等关系列不等式组,即可求得通话的时间范围,从而求得结果.
(1)A 地位置如图所示:
![]()
使点A满足AB∶AC=2∶3;
(2)乙车的速度150÷2=75千米/时,
![]() ,
,
∴M(1.2,0)
∴点 M表示乙车 1.2 小时到达 A地;
(3)甲车的函数图象如图所示:
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() .
.
(4)由题意得![]() ,
,
解得![]() ;
;
![]() ,
,
解得![]() .
.
∴![]()
∴两车同时与指挥中心通话的时间为![]() 小时.
小时.


科目:初中数学 来源: 题型:
【题目】下列说法不正确的是( )
A. 某种彩票中奖的概率是![]() ,买1000张该种彩票一定会中奖
,买1000张该种彩票一定会中奖
B. 了解一批电视机的使用寿命适合用抽样调查
C. 若甲组数据方差![]() =0.39,乙组数据方差
=0.39,乙组数据方差![]() =0.27,则乙组数据比甲组数据稳定
=0.27,则乙组数据比甲组数据稳定
D. 在一个装有白球和绿球的袋中摸球,摸出黑球是不可能事件
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年的6月5日为世界环保日,为了提倡低碳环保,某公司决定购买10台节省能源的新设备,现有甲、乙两种型号的设备可供选购. 经调查:购买3台甲型设备比购买2台乙型设备多花16万元,购买2台甲型设备比购买3台乙型设备少花6万元.
(1)求甲、乙两种型号设备的价格;
(2)该公司经预算决定购买节省能源的新设备的资金不超过110万元,你认为该公司有哪几种购买方案;
(3)在(2)的条件下,已知甲型设备的产量为240吨/月,乙型设备的产量为180吨/月.若每月要求总产量不低于2040吨,为了节约资金,请你为该公司设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,CA=CB,∠ACB=90°,AB=4,点D为AB的中点,以点D为圆心作圆,半圆恰好经过三角形的直角顶点C,以点D为顶点,作90°的∠EDF,与半圆交于点E,F,则图中阴影部分的面积是____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,B的坐标分别为(-4,5),(-2,1).

(1)写出点C及点C关于y轴对称的点C′的坐标;
(2)请作出△ABC关于y轴对称的△A′B′C′;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(类比概念)三角形的内切圆是以三个内角的平分线的交点为圆心,以这点到三边的距离为半径的圆,则三角形可以称为圆的外切三角形,可以得出三角形的三边与该圆相切.以此类推,如图1,各边都和圆相切的四边形称为圆外切四边形
(性质探究)如图1,试探究圆外切四边形的ABCD两组对边AB,CD与BC,AD之间的数量关系
猜想结论: (要求用文字语言叙述)
写出证明过程(利用图1,写出已知、求证、证明)
(性质应用)
①初中学过的下列四边形中哪些是圆外切四边形 (填序号)
A:平行四边形:B:菱形:C:矩形;D:正方形
②如图2,圆外切四边形ABCD,且AB=12,CD=8,则四边形的周长是 .
③圆外切四边形的周长为48cm,相邻的三条边的比为5:4:7,求四边形各边的长.
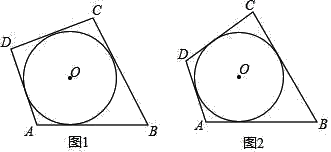
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利45元,为了扩大销售、增加盈利尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出4件,若商场平均每天盈利2100元,每件衬衫应降价多少元?请完成下列问题:
(1)未降价之前,某商场衬衫的总盈利为 元.
(2)降价后,设某商场每件衬衫应降价x元,则每件衬衫盈利 元,平均每天可售出 件(用含x的代数式进行表示)
(3)请列出方程,求出x的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com