
����Ŀ����ͼ����A��ԭ����������������˶���ͬʱ����BҲ��ԭ����������������˶���3����������15����λ����.��֪��B���ٶ��ǵ�A���ٶȵ�4�����ٶȵ�λ����λ����/�룩.
![]()
��1�������A����B�˶����ٶȣ����������ϱ��A��B�����ԭ������˶�3��ʱ��λ�ã�
��2����A��B�����(1)�е�λ�ÿ�ʼ������ԭ�����ٶ�ͬʱ�����������˶�������ʱ��ԭ��ǡ�ô��ڵ�A����B�����м䣿
��3����A��B�����(1)�е�λ�ÿ�ʼ������ԭ�����ٶ�ͬʱ�����������˶�ʱ����һ��Cͬʱ��B��λ�ó�����A���˶���������A�������������B���˶�������B���������������A���˶������������ֱ��B����A��ʱ��C������ֹͣ�˶�.����Cһֱ��20��λ����/����ٶ������˶�����ô��C�ӿ�ʼ�˶���ֹͣ�˶�����ʻ��·���Ƕ��ٸ���λ���ȣ�
���𰸡���1����A���ٶ�Ϊÿ��1����λ����, ��B���ٶ�Ϊÿ��4����λ���ȣ�A��B����λ�ü���������2���˶�1.8��ʱ��ԭ��ǡ�ô���A��B��������м䣻��3��100����λ����.
��������
��1�����A���ٶ�Ϊÿ��t����λ���ȣ����B���ٶ�Ϊÿ��4t����λ���ȣ����������г����̿���õ�A���ٶȺ͵�B���ٶȣ�Ȼ���������ϱ��λ�ü��ɣ�
��2������ԭ��ǡ�ô��ڵ�A����B�����м��з�����⼴�ɣ�
��3���������B�ϵ�A�����ʱ�䣬Ȼ�����·�̣��ٶ���ʱ�����.
�⣺��1�����A���ٶ�Ϊÿ��t����λ���ȣ����B���ٶ�Ϊÿ��4t����λ���ȣ�
��������3t+3��4t=15�����t=1��
���A���ٶ�Ϊÿ��1����λ���ȣ���B���ٶ�Ϊÿ��4����λ���ȣ�
A��B����λ�����£�
![]() ��
��
��2����x��ʱ��ԭ��ǡ�ô��ڵ�A����B�����м䣬
�������⣬��3+x=12-4x��
��֮�ã�x=1.8��
���˶�1.8��ʱ��ԭ��ǡ�ô���A��B��������м䣻
��3�����˶�y��ʱ����B�ϵ�A��
��������ã�4y-y=15��
��ã�y=5��
����B�ϵ�A����ȥ5�룬�����ʱ��ǡ���ǵ�C�ӿ�ʼ�˶���ֹͣ�˶�������ʱ�䣬��˵�C��ʻ��·��Ϊ��20��5=100(��λ����).


 ��ս100��Ԫ����Ծ�ϵ�д�
��ս100��Ԫ����Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
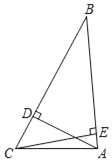
����Ŀ������ǡ�ABC�У�AD��CE�ֱ��DZ�BC��AB�ĸߣ�AB��12��BC��16��S��ABC��48��
��(1)��B�Ķ�����
(2)tanC��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����A����B�������ϣ���C��ʾ������3��5������D��ʾ��(��2)����E��ʾ��2![]() ��
��
![]()
��1����A��ʾ_______����B��ʾ_______��
��2���������ϱ�ʾ����C����D����E��
��3)�Ƚϴ�С��_______��_______��_______��_______��_______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������Ҫ����һ�γ����β���������һЩ�ͺ���ͬ�Ļ�ɫ�����ε�ש��һЩ�ͺ���ͬ �İ�ɫ����ֱ�������ε�ש����ͼ��ʾ��ʽ����.

��1�� �����������ε�ש40�飬����ʹ�������ε�ש____________�飻
��2�� �����������ε�ש2 020�飬����ʹ�������ε�ש____________��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ���꼶ȫ��ѧ����5����ʦ�Ĵ�����ȥ�����Σ�������ƱΪÿ��30Ԫ.���������Żݷ�����������������ʦ��ѣ�ѧ����8���շѣ��ҷ�����ʦ������7.5���շ�.
��1������n��ѧ�����ú�n�Ĵ���ʽ��ʾ�����Żݷ����������Ԫ��
��2����n=70ʱ���������ַ������Żݣ�
��3����n=100ʱ���������ַ������Żݣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����m��n����ʵ����������m+n=mnʱ���ͳƵ�P��m��![]() ��Ϊ��������������֪��A��0��5�����M����ֱ��y=��x+b�ϣ���B��C���������������ҵ�B���߶�AM�ϣ���MC=
��Ϊ��������������֪��A��0��5�����M����ֱ��y=��x+b�ϣ���B��C���������������ҵ�B���߶�AM�ϣ���MC=![]() ��AM=4
��AM=4![]() �����MBC�����
�����MBC�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2019��С��ǰ����µĽ���仯������±���������ʾ��ǰһ�¶��Ǯ����������ʾ��ǰһ���ٵ�Ǯ������λ��Ԫ��
�·� | һ�� | ���� | ���� | ���� | ���� |
Ǯ���仯 |
|
|
|
|
|
��2018��12�·�С�ŵĽ���Ϊ![]() Ԫ.
Ԫ.
��1���ô���ʽ��ʾ2019����·�С�ŵĽ���Ϊ___________Ԫ��
��2��С�����·����ý���ȶ��·ݶ���٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
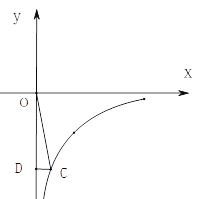
����Ŀ����ͼ����C�ڷ���������y=![]() ��ͼ���ϣ�����C��CD��y�ᣬ��y�Ḻ�����ڵ�D������ODC�������3��
��ͼ���ϣ�����C��CD��y�ᣬ��y�Ḻ�����ڵ�D������ODC�������3��
��1����������y=![]() �Ľ���ʽ��
�Ľ���ʽ��
��2����CD=1����ֱ��OC�Ľ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD��DEFG����������������AE��CG.

(1)��֤��AE=CG��
(2)�۲�ͼ��������AE��CG֮���λ�ù�ϵ����֤����IJ���.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com