C
分析:把a,b,c中的两个字母的和当作一个整体,由于a+b+c=16,16是偶数,根据偶数+偶数=偶数,奇数+奇数=偶数,偶数+奇数=奇数,而2是唯一的偶质数,得出a,b,c中有一个是2,不妨设a=2,则b+c=14,且b、c都是奇质数,再根据三角形三边关系定理得出b、c的值,利用勾股定理求出
解答:∵a+b+c=16,a,b,c都是质数,则a,b,c的值一定是:1或2或3或5或7或11或13.
∴a,b,c中有一个是2,根据大边对大角可得:a=2,
∴b+c=14,且b、c都是奇质数,
又∵14=3+11=7+7,
而2+3<11,
∴以2,3,11为边不能组成三角形;
而2+7>7,
以2,7,7为边能组成三角形.
画出示意图如下:
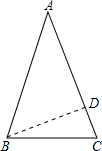
设AD=x,则DC=7-x,
∵AB
2-AD
2=BC
2-CD
2,即7
2-x
2=2
2-(7-x)
2,
解得x=

,即AD=

,
∴cosA=
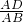
=
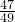
.
故选C.
点评:本题考查了奇偶数、质数的有关知识及三角形三边关系定理,难度较大,其中对于奇偶数、质数的有关知识考查属于竞赛题型,超出教材大纲要求范围.


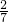
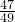

 ,即AD=
,即AD= ,
,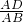 =
=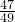 .
.
