
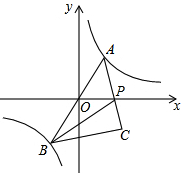
 如图,反比例函数y=$\frac{k}{x}$的图象经过点(-$\sqrt{2}$,-4),点A是该图象第一象限分支上的动点,连结AO并延长交另一分支于点B,以AB为斜边作等腰直角三角形ABC,顶点C在第四象限,AC与x轴交于点P,连结BP.在点A运动过程中,当BP平分∠ABC时,点C的坐标是(2$\sqrt{2}$,-2).
如图,反比例函数y=$\frac{k}{x}$的图象经过点(-$\sqrt{2}$,-4),点A是该图象第一象限分支上的动点,连结AO并延长交另一分支于点B,以AB为斜边作等腰直角三角形ABC,顶点C在第四象限,AC与x轴交于点P,连结BP.在点A运动过程中,当BP平分∠ABC时,点C的坐标是(2$\sqrt{2}$,-2). 分析 连接OC,过点A作AE⊥x轴于E,过点C作CF⊥x轴于F,则有△AOE≌△OCF,进而可得出AE=OF、OE=CF,根据角平分线的性质可得出$\frac{CP}{AP}$=$\frac{CF}{AE}$=$\frac{BC}{AB}$=$\frac{1}{\sqrt{2}}$,即$\frac{OE}{AE}$=$\frac{\sqrt{2}}{2}$,由反比例函数图象上点的坐标特征可求出k值,设点A的坐标为(a,$\frac{4\sqrt{2}}{a}$)(a>0),由$\frac{OE}{AE}$=$\frac{\sqrt{2}}{2}$可求出a值,由此即可得出CF、OF的长度,结合图形即可得出点C的坐标.
解答 解:连接OC,过点A作AE⊥x轴于E,过点C作CF⊥x轴于F,如图所示.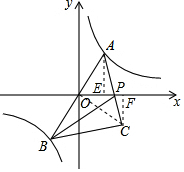
∵△ABC为等腰直角三角形,
∴OA=OC,OC⊥AB,
∴∠AOE+∠COF=90°.
∵∠COF+∠OCF=90°,
∴∠AOE=∠OCF.
在△AOE和△OCF中,$\left\{\begin{array}{l}{∠AEO=∠OFC=90°}\\{∠AOE=∠OCF}\\{OA=CO}\end{array}\right.$,
∴△AOE≌△OCF(AAS),
∴AE=OF,OE=CF.
∵BP平分∠ABC,
∴$\frac{CP}{AP}$=$\frac{CF}{AE}$=$\frac{BC}{AB}$=$\frac{1}{\sqrt{2}}$,
∴$\frac{OE}{AE}$=$\frac{\sqrt{2}}{2}$.
∵反比例函数y=$\frac{k}{x}$的图象经过点(-$\sqrt{2}$,-4),
∴k=-$\sqrt{2}$×(-4)=4$\sqrt{2}$,
∴设点A的坐标为(a,$\frac{4\sqrt{2}}{a}$)(a>0),
∴$\frac{a}{\frac{4\sqrt{2}}{a}}$=$\frac{\sqrt{2}}{2}$,解得:a=2或a=-2(舍去),
∴CF=OE=a=2,OF=AE=$\frac{4\sqrt{2}}{a}$=2$\sqrt{2}$.
∴点C的坐标为(2$\sqrt{2}$,-2).
故答案为:(2$\sqrt{2}$,-2).
点评 本题考查了反比例函数图象上点的坐标特征、全等三角形的判定与性质、角平分线的性质以及等腰直角三角形,构造全等三角形,找出CF、OF的长度是解题的关键.


科目:初中数学 来源: 题型:解答题
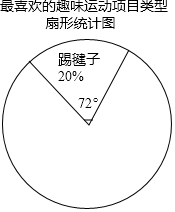 某校为更好的开展“冬季趣味运动会”活动,随机在各年级抽查了部分学生,了解他们最喜爱的趣味运动项目类型(跳长绳、踢毽子、背夹球、拔河共四类),并将统计结果绘制成如图不完整的频数分布表.
某校为更好的开展“冬季趣味运动会”活动,随机在各年级抽查了部分学生,了解他们最喜爱的趣味运动项目类型(跳长绳、踢毽子、背夹球、拔河共四类),并将统计结果绘制成如图不完整的频数分布表.| 项目类型 | 频数 | 频率 |
| 跳长绳 | 25 | a |
| 踢毽子 | 20 | 0.2 |
| 背夹球 | b | 0.4 |
| 拔河 | 15 | 0.15 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
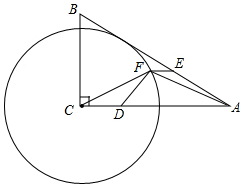 如图,在Rt△ABC中,∠A=30°,AC=8,以C为圆心,4为半径作⊙C.
如图,在Rt△ABC中,∠A=30°,AC=8,以C为圆心,4为半径作⊙C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
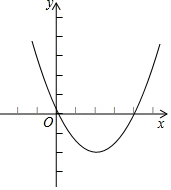 在平面直角坐标系xOy中,直线y=ax+b与抛物线y=ax2+bx交于A、B两点(点A在点B的左侧),点C的坐标为(a,b).
在平面直角坐标系xOy中,直线y=ax+b与抛物线y=ax2+bx交于A、B两点(点A在点B的左侧),点C的坐标为(a,b).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
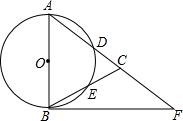 如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E.点F在AC的延长线上,且∠CBF=$\frac{1}{2}$∠CAB.
如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E.点F在AC的延长线上,且∠CBF=$\frac{1}{2}$∠CAB.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
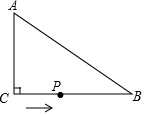 如图,在△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点C出发,按C→B→A的路径,以2cm每秒的速度运动,设运动时间为t秒,当t为3或6或6.5或5.4时,△ACP是等腰三角形.
如图,在△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点C出发,按C→B→A的路径,以2cm每秒的速度运动,设运动时间为t秒,当t为3或6或6.5或5.4时,△ACP是等腰三角形.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ① | B. | ② | C. | ③ | D. | ④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系中xOy中,抛物线y=$\frac{1}{2}$x2-mx+$\frac{1}{2}$m2+m-2的顶点在x轴上.
在平面直角坐标系中xOy中,抛物线y=$\frac{1}{2}$x2-mx+$\frac{1}{2}$m2+m-2的顶点在x轴上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com