
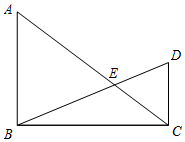
 已知:如图,在Rt△ABC和Rt△BCD中,∠ABC=∠BCD=90°,BD与AC相交于点E,AB=9,cos∠BAC=$\frac{3}{5}$,tan∠DBC=$\frac{5}{12}$.
已知:如图,在Rt△ABC和Rt△BCD中,∠ABC=∠BCD=90°,BD与AC相交于点E,AB=9,cos∠BAC=$\frac{3}{5}$,tan∠DBC=$\frac{5}{12}$.分析 (1)根据题目中的数据和锐角三角函数可以求得CD的长;
(2)根据题意可以求得BC和BC边上的高,从而可以求得△BCE的面积.
解答 解:(1)∵∠ABC=∠BCD=90°,AB=9,cos∠BAC=$\frac{3}{5}$,tan∠DBC=$\frac{5}{12}$,
∴设CD=5a,则BC=12a,AB=9a,
∴9a=9,得a=1,
∴CD=5a=5,
即CD的长是5;
(2)由(1)知,AB=9,BC=12,CD=5,
∵∠ABC=∠BCD=90°,
∴AB∥CD,
∴$\frac{CE}{AE}=\frac{CD}{AB}=\frac{5}{9}$,
作EF∥AB交CB于点F,
则△CEF∽△CAB,
∴$\frac{CE}{CA}=\frac{EF}{AB}$,
∴$\frac{5}{14}=\frac{EF}{9}$,
解得,EF=$\frac{45}{14}$,
∴△BCE的面积是:$\frac{BC•EF}{2}=\frac{12×\frac{45}{14}}{2}=\frac{135}{7}$.
点评 本题考查解直角三角形,解答本题的关键是明确题意,找出所求问题需要的条件,利用锐角三角函数和勾股定理解答.


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
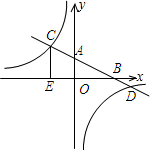 如图,在平面直角坐标系xOy中,一次函数y1=ax+b的图象分别与x,y轴交于点B,A,与反比例函数y2=$\frac{m}{x}$的图象交于点C,D,CE⊥x轴于点E,tan∠ABO=$\frac{1}{2}$,OB=4,OE=2.
如图,在平面直角坐标系xOy中,一次函数y1=ax+b的图象分别与x,y轴交于点B,A,与反比例函数y2=$\frac{m}{x}$的图象交于点C,D,CE⊥x轴于点E,tan∠ABO=$\frac{1}{2}$,OB=4,OE=2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
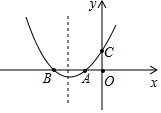 如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于点C,且OA=OC,给出下列结论:
如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于点C,且OA=OC,给出下列结论:| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
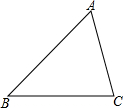 为落实中央提出绿色发展的理念,某环保部门对A、B、C三个企业的污水进行集中处理,计划在道路AB上建立一个污水处理站D,使得到这三个企业铺设的污水管道总长度最短.已知∠ABC=45°,∠ACB=75°,AC=20千米,在图中画出污水处理站D的位置,并求所铺设的管道总长度(结果保留根号).
为落实中央提出绿色发展的理念,某环保部门对A、B、C三个企业的污水进行集中处理,计划在道路AB上建立一个污水处理站D,使得到这三个企业铺设的污水管道总长度最短.已知∠ABC=45°,∠ACB=75°,AC=20千米,在图中画出污水处理站D的位置,并求所铺设的管道总长度(结果保留根号).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com