练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
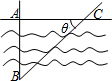
    12．如图，为了测量河两岸A、B两点的距离，在与AB垂直的方向点C处测得AC=a，∠ACB=θ，那么AB等于（　　）
    A．a•sinθB．a•tanθC．a•cosθD．$\frac{a}{tanθ}$

    分析 根据题意，可得Rt△ABC，同时可知AC与∠ACB．根据三角函数的定义解答．

    解答 解：根据题意，在Rt△ABC，AC=a，∠ACB=θ，且tanα=$\frac{AB}{AC}$，
    则AB=AC×tanα=a•tanθ，
    故选B．

    点评 本题考查了解直角三角形的应用，熟练掌握三角函数的定义是解决问题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2016-2017学年江苏省东台市第六教育联盟七年级下学期第一次月考数学试卷 题型：解答题

    如图：在正方形网格中有一个△ABC，按要求进行下列作图（只能借助于网格）．

    （1）画出△ABC中BC边上的高AG和BC边上的中线AE．

    （2）画出先将△ABC向右平移5格，再向上平移3格后的△DEF．

    （3）△ABC的面积为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．如图1，矩形ABCD的边AB=4，BC=7，EA平分∠BAD交BC于E，连接DE，在矩形内部作边长为2的正方形FGHI，使得HI与BC共线，点I与点B重合，将正方形FGHI沿BC向右平移，平移速度为每秒1个单位长度，当GH与CD重合时停止运动，设运动过程中正方形FGHI与△AED的重叠部分面积为s，运动时间为t（t＞0）．

    （1）求使点G落在线段DE上的时间t；
    （2）求出在正方形FGHI向右平移过程中s关于t的函数关系式，并写出对应t的取值范围；
    （3）如图2，将矩形ABCD沿DE翻折，翻折后点D与点D′对应，点C与点C′对应，再将所得△C′D′E绕着点E旋转，直线C′D′与射线ED交于点P，当△C′DP为等腰三角形时，直接写出PD′的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．如图①，在平面直角坐标系中，OA=6，以OA为边长作等边三角形ABC，使得BC∥OA，且点B、C落在过原点且开口向下的抛物线上．
    （1）求这条抛物线的解析式；
    （2）在图①中，假设一动点P从点B出发，沿折线BAC的方向以每秒2个单位的速度运动，同时另一动点Q从O点出发，沿x轴的负半轴方向以每秒1个单位的速度运动，当点P运动到A点时，P、Q都同时停止运动，在P、Q的运动过程中，是否存在时间t，使得PQ⊥AB，若存在，求出t的值，若不存在，请说明理由；
    （3）在BC边上取两点E、F，使BE=EF=1个单位，试在AB边上找一点G，在抛物线的对称轴上找一点H，使得四边形EGHF的周长最小，并求出周长的最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．先化简，再求值：（$\frac{a-1}{{a}^{2}-4a+4}$-$\frac{a+2}{{a}^{2}-2a}$）÷（$\frac{4}{a}$-1），其中a=1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．先化简$\frac{1+x}{{{x^2}+x-2}}÷（x-2+\frac{3}{x+2}）$，再选一个你喜欢的数代入求值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．有两张完全重合的矩形纸片，将其中一张绕点A顺时针旋转90°后得到矩形AMEF（如图1），连接BD，MF，若BD=8cm，∠ADB=30°．

    （1）试探究线段BD与线段MF的关系，并简要说明理由；
    （2）把△BCD与△MEF剪去，将△ABD绕点A顺时针旋转得△AB1D1，边AD1交FM于点K（如图2），设旋转角为β（0°＜β＜90°），当△AFK为等腰三角形时，求β的度数；
    （3）若将△AFM沿AB方向平移得到△A2F2M2（如图3），F2M2与AD交于点P，A2M2与BD交于点N，当NP∥AB时，求平移的距离．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    1．（x2-mx+3）（3x-2）的积中不含x的二次项，则m的值是-$\frac{2}{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．从1，3，-4这三个数中，随机抽取两个数相乘，积是正数的概率是（　　）
    A．$\frac{1}{2}$B．$\frac{1}{3}$C．$\frac{2}{3}$D．$\frac{3}{4}$

    查看答案和解析>>

    同步练习册答案