
 如图,在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按图中“→“方向排列,如(1,0),(2,0),(2,1),(1,1),(1,2),(2,2)…根据这个规律,第82个点的坐标(10,0).
如图,在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按图中“→“方向排列,如(1,0),(2,0),(2,1),(1,1),(1,2),(2,2)…根据这个规律,第82个点的坐标(10,0). 分析 观察图形可知,以最外边的矩形边长上的点为准,点的总个数等于x轴上右下角的点的横坐标的平方,并且右下角的点的横坐标是奇数时最后以横坐标为该数,纵坐标为0结束,当右下角的点横坐标是偶数时,以横坐标为1,纵坐标为右下角横坐标的偶数减1的点结束,根据此规律解答即可.
解答 解:根据图形,以最外边的矩形边长上的点为准,点的总个数等于x轴上右下角的点的横坐标的平方,
例如:右下角的点的横坐标为1,共有1个,1=12,
右下角的点的横坐标为2时,共有4个,4=22,
右下角的点的横坐标为3时,共有9个,9=32,
右下角的点的横坐标为4时,共有16个,16=42,
…
右下角的点的横坐标为n时,共有n2个,
∵92=81,9是奇数,
∴第82个点是(10,0),
故答案为:(10,0).
点评 本题考查了点的坐标,观察出点个数与横坐标的存在的平方关系是解题的关键.


科目:初中数学 来源: 题型:填空题
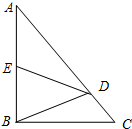 如图,在Rt△ABC中,∠ABC=90°,点D在边AC上,线段DB绕点D顺时针旋转,端点B恰巧落在边AB上的点E处.如果$\frac{AE}{EB}$=y,$\frac{AD}{DC}$=x.那么y与x满足的关系式是:y=$\frac{x-1}{2}$(用含x的代数式表示y).
如图,在Rt△ABC中,∠ABC=90°,点D在边AC上,线段DB绕点D顺时针旋转,端点B恰巧落在边AB上的点E处.如果$\frac{AE}{EB}$=y,$\frac{AD}{DC}$=x.那么y与x满足的关系式是:y=$\frac{x-1}{2}$(用含x的代数式表示y).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
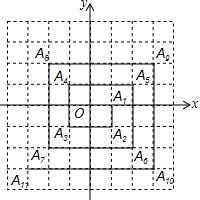 如图,已知A1(1,0),A2(1,-1),A3(-1,-1),A4(-1,1),A5(2,1),…,则点A2014的坐标是(504,-504).
如图,已知A1(1,0),A2(1,-1),A3(-1,-1),A4(-1,1),A5(2,1),…,则点A2014的坐标是(504,-504).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
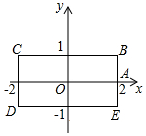 如图,长方形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙分别由点A(2,0)同时出发,沿长方形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2015次相遇地点的坐标是( )
如图,长方形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙分别由点A(2,0)同时出发,沿长方形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2015次相遇地点的坐标是( )| A. | (2,0) | B. | (-1,1) | C. | (-2,1) | D. | (-1,-1) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
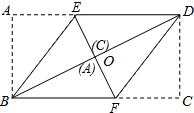 如图,将矩形纸片ABCD沿BE、DF折叠后,顶点A、C恰好都落在对角线BD的中点O处.若BD=6cm,则四边形BEDF的周长是8$\sqrt{3}$cm.
如图,将矩形纸片ABCD沿BE、DF折叠后,顶点A、C恰好都落在对角线BD的中点O处.若BD=6cm,则四边形BEDF的周长是8$\sqrt{3}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知点P是线段AB的黄金分割点,且AP>PB,设以AP为边长的正方形ACDP的面积为S1,以BF,AB的长为邻边的矩形AEFB的面积为S2,BF=PB,试问S1与S2有何关系?
如图,已知点P是线段AB的黄金分割点,且AP>PB,设以AP为边长的正方形ACDP的面积为S1,以BF,AB的长为邻边的矩形AEFB的面积为S2,BF=PB,试问S1与S2有何关系?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com