
【题目】在平面直角坐标系xOy中的点Q,我们记点Q到横轴的距离为d1,到纵轴的距离为d2,规定:若d1≥d2,则称d1为点Q的“系长距”;若d1<d2,则称d2为点Q的“系长距”
例如:点Q(3,﹣4)到横轴的距离d1=4,到纵轴的距离d2=3,因为4>3,所以点Q的系长距”为4

(1)①点A(﹣6,2)的“系长距”为 ;②若点B(a,2)的“系长距”为4,则a的值为 .
(2)已知A(3,0),B(0,4),点P为线段AB上的一点,且PB:PA=2:3,点P的“系长距”.
(3)若点C在双曲线y=![]() 上,且点C的“系长距”为6,求点C的坐标.
上,且点C的“系长距”为6,求点C的坐标.
【答案】(1)①6;②±4;(2)![]() ;(3)(6,
;(3)(6, ![]() )或(﹣6,﹣
)或(﹣6,﹣![]() )或(
)或(![]() ,6)或(﹣
,6)或(﹣![]() ,﹣6).
,﹣6).
【解析】
(1)根据“系长距”的定义即可得到结论;
(2)根据勾股定理得到AB=5,过P作PE⊥OA于E,PF⊥OB于F,根据相似三角形的性质得到P(![]() ,
,![]() ),根据“系长距”的定义即可得到结论;
),根据“系长距”的定义即可得到结论;
(3)设点C的坐标(x,y),由点C的“系长距”为6,得到x=±6或y=±6,分别代入反比例函数的解析式即可得到结论.
解:(1)①∵点A(﹣6,2)到横轴的距离d1=2,到纵轴的距离d2=6,因为6>2,所以点A的“系长距“为:6;
故答案为:6;
②∵点B(a,2)的“系长距”为4,
∴a的值为±4,
故答案为:±4;
(2)如图,
∵A(3,0),B(0,4),
∴OA=3,OB=4,
∴AB=5,
过P作PE⊥OA于E,PF⊥OB于F,

∴PF∥OA,PE∥OB,
∴△PBF∽△BAO,△APE∽△ABO,
∴![]() ,
,![]() ,
,
∵PB:PA=2:3,
∴PB:AB=2:5,PA:AB=3:5,
∴PE=![]() ,PF=
,PF=![]()
∴P(![]() ,
,![]() ),
),
∴点P的“系长距”为:![]() ;
;
(3)设点C的坐标(x,y),
∵点C的“系长距”为6,
∴x=±6或y=±6,
当x=6时,y=![]() ,此时点C的坐标为(6,
,此时点C的坐标为(6,![]() ),
),
当x=﹣6时,y=![]() ,此时点C的坐标为(﹣6,
,此时点C的坐标为(﹣6,![]() ),
),
当y=6时,6=![]() ,x=
,x=![]() ,此时点C的坐标为(
,此时点C的坐标为(![]() ,6),
,6),
当y=﹣6时,﹣6=![]() ,x=
,x=![]() ,此时点C的坐标为(
,此时点C的坐标为(![]() ,﹣6),
,﹣6),
综上所述,点C的坐标为(6,![]() )或(﹣6,
)或(﹣6,![]() )或(
)或(![]() ,6)或(
,6)或(![]() ,﹣6).
,﹣6).


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C,D是⊙O上的点,且OC∥BD,AD分别与BC,OC相交于点E,F,则下列结论:
①AD⊥BD;②∠AOC=∠AEC;③CB平分∠ABD;④AF=DF;⑤BD=2OF;⑥△CEF≌△BED,其中一定成立的是( )
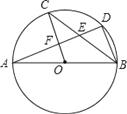
A. ②④⑤⑥ B. ①③⑤⑥ C. ②③④⑥ D. ①③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着移动互联网的快速发展,基于互联网的共享单车应运而生.为了解某小区居民使用共享单车的情况,某研究小组随机采访该小区的10位居民,得到这10位居民一周内使用共享单车的次数分别为:17,12,15,20,17,0,7,26,17,9.
(1)这组数据的中位数是 ,众数是 ;
(2)计算这10位居民一周内使用共享单车的平均次数;
(3)若该小区有200名居民,试估计该小区居民一周内使用共享单车的总次数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠C=90°,AC=BC,将△ABC绕点A顺时针方向旋转60°到△AB'C'的位置,连接C′B,C′B=![]() ﹣1,则AC=_____.
﹣1,则AC=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABO中,AB⊥OB,OB=![]() ,AB=1,把△ABO绕点O旋转150°后得到△A1B1O,则点A1的坐标为
,AB=1,把△ABO绕点O旋转150°后得到△A1B1O,则点A1的坐标为
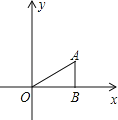
A.(﹣1,![]() ) B.(﹣1,
) B.(﹣1,![]() )或(﹣2,0) C.(
)或(﹣2,0) C.(![]() ,﹣1)或(0,﹣2) D.(
,﹣1)或(0,﹣2) D.(![]() ,﹣1)
,﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,扇形OAB中,∠AOB=90°.P为弧AB上的一点,过点P作PC⊥OA,垂足为C,PC与AB交于点D.若PD=2,CD=1,则该扇形的半径长为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
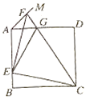
【题目】如图,正方形ABCD的边长为a,点E在边AB上运动(不与点A,B重合),∠DAM=45°,点F在射线AM上,且![]() ,CF与AD相交于点G,连接EC,EF,EG,则下列结论:①∠ECF=45°;②
,CF与AD相交于点G,连接EC,EF,EG,则下列结论:①∠ECF=45°;②![]() 的周长为
的周长为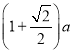 ;③
;③![]() ;④
;④![]() 的面积的最大值
的面积的最大值![]() .其中正确的结论是____.(填写所有正确结论的序号)
.其中正确的结论是____.(填写所有正确结论的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com