
 如图,已知Rt△AOB中,∠AOB=90°,AO=6,BO=4,点E、M是线段AB上的两个不同的动点(不与端点重合),分别过E、M作AO的垂线,垂足分别为K、L.
如图,已知Rt△AOB中,∠AOB=90°,AO=6,BO=4,点E、M是线段AB上的两个不同的动点(不与端点重合),分别过E、M作AO的垂线,垂足分别为K、L.分析 (1)根据条件证明△OBA∽△KEA,得到比例式,用含OK的式子表示KE,根据三角形的面积公式,列出关于OK的关系式即可;
(2)根据菱形的性质和勾股定理,利用一元二次方程根与系数的关系,求出答案.
解答 解:(1)如图,∵EK⊥OA,∠AOB=90°,
∴△OBA∽△KEA,
∴$\frac{OB}{KE}=\frac{OA}{KA}$,即 $\frac{4}{KE}=\frac{6}{6-OK}$,
∴KE=$\frac{2(6-OK)}{3}$,
∴S=$\frac{1}{2}$×OK•KE=$\frac{1}{2}$×OK×$\frac{2(6-OK)}{3}$,
设OK=x,则S=$\frac{1}{2}$×x×$\frac{2(6-x)}{3}$=$-\frac{1}{3}{x}^{2}+2x$,
∴当x=3 时,S有最大值,最大值=-3+6=3;
(2)如图,当EM⊥OF时,平行四边形EOMF为菱形,OE的取值范围为$\frac{12}{13}\sqrt{13}$<OE<4,
设OK=a,OL=b,
由(1)得,KE=$\frac{2(6-a)}{3}$,ML=$\frac{2(6-b)}{3}$,
由OE=OM得,
a2+[$\frac{2(6-a)}{3}$]2=b2+[$\frac{2(6-b)}{3}$]2.
若设y=x2+[$\frac{2(6-x)}{3}$]2=$\frac{13}{9}$x2-$\frac{16}{3}$ x+16,则
当x1=a,x2=b时,函数y的值相等.
∵函数y的对称轴为直线x=$\frac{{x}_{1}+{x}_{2}}{2}$=$\frac{24}{13}$,
∴$\frac{a+b}{2}$=$\frac{24}{13}$,
解得a+b=$\frac{48}{13}$,即OK+OL=$\frac{48}{13}$.
故答案为:(1)3;(2)$\frac{48}{13}$.
点评 本题综合考查了菱形的性质、相似三角形的判定和性质、一元二次方程以及二次函数的应用,综合性很强,属于较难题.解题时注意:对角线互相垂直的平行四边形为菱形.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案科目:初中数学 来源: 题型:填空题
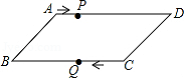 如图,平行四边形ABCD中,AB=8cm,AD=12cm,点P在AD边上以每秒1cm 的速度从点A向点D运动,点Q在BC边上,以每秒4cm的速度从点C出发,在CB间往返运动,两个点同时出发,当点P到达点D时停止(同时点Q也停止),在运动以后,以P、D、Q、B四点组成平行四边形的次数有3次.
如图,平行四边形ABCD中,AB=8cm,AD=12cm,点P在AD边上以每秒1cm 的速度从点A向点D运动,点Q在BC边上,以每秒4cm的速度从点C出发,在CB间往返运动,两个点同时出发,当点P到达点D时停止(同时点Q也停止),在运动以后,以P、D、Q、B四点组成平行四边形的次数有3次.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,平行四边形ABCD中,AB>AD,AE,BE,CM,DM分别为∠DAB,∠ABC,∠BCD,∠CDA的平分线,AE与DM相交于点F,BE与CM相交于点N,连接EM.若平行四边形ABCD的周长为42,FM=3,EF=4,则AB的长为( )
如图,平行四边形ABCD中,AB>AD,AE,BE,CM,DM分别为∠DAB,∠ABC,∠BCD,∠CDA的平分线,AE与DM相交于点F,BE与CM相交于点N,连接EM.若平行四边形ABCD的周长为42,FM=3,EF=4,则AB的长为( )| A. | 11 | B. | 12 | C. | 13 | D. | 14 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 8.18×108 | B. | 81.8×109 | C. | 8.18×1010 | D. | 0.818×109 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com