
【题目】如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作ABDE,连接AD,EC.
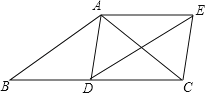
(1)求证:△ADC≌△ECD;
(2)若BD=CD,求证:四边形ADCE是矩形.
【答案】(1)见解析;(2)继续剪
【解析】
试题分析:(1)根据平行四边形的性质、等腰三角形的性质,利用全等三角形的判定定理SAS可以证得△ADC≌△ECD;
(2)利用等腰三角形的“三合一”性质推知AD⊥BC,即∠ADC=90°;由平行四边形的判定定理(对边平行且相等是四边形是平行四边形)证得四边形ADCE是平行四边形,所以有一个角是直角的平行四边形是矩形.
证明:(1)∵四边形ABDE是平行四边形(已知),
∴AB∥DE,AB=DE(平行四边形的对边平行且相等);
∴∠B=∠EDC(两直线平行,同位角相等);
又∵AB=AC(已知),
∴AC=DE(等量代换),∠B=∠ACB(等边对等角),
∴∠EDC=∠ACD(等量代换);
∵在△ADC和△ECD中,
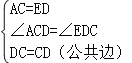 ,
,
∴△ADC≌△ECD(SAS);
(2)∵四边形ABDE是平行四边形(已知),
∴BD∥AE,BD=AE(平行四边形的对边平行且相等),
∴AE∥CD;
又∵BD=CD,
∴AE=CD(等量代换),
∴四边形ADCE是平行四边形(对边平行且相等的四边形是平行四边形);
在△ABC中,AB=AC,BD=CD,
∴AD⊥BC(等腰三角形的“三合一”性质),
∴∠ADC=90°,
∴ADCE是矩形.


科目:初中数学 来源: 题型:
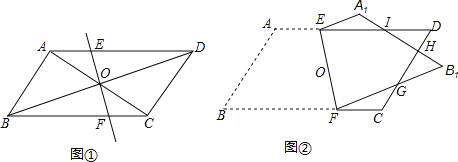
【题目】(1)如图①,ABCD的对角线AC,BD交于点O,直线EF过点O,分别交AD,BC于点E,F.求证:AE=CF.
(2)如图②,将ABCD(纸片)沿过对角线交点O的直线EF折叠,点A落在点A1处,点B落在点B1处,设FB1交CD于点G,A1B1分别交CD,DE于点H,I.求证:EI=FG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O(0,0),A(0,1)是正方形OAA1B的两个顶点,以OA1对角线为边作正方形OA1A2B1,再以正方形的对角线OA2作正方形OA1A2B1,…,依此规律,则点A8的坐标是( )
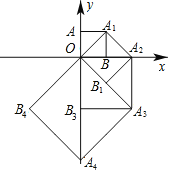
A.(﹣8,0) B.(0,8) C.(0,8![]() ) D.(0,16)
) D.(0,16)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件是必然事件的是( )
A. 抛掷一枚硬币四次,有二次正面朝上 B. 打开电视频道,正在播放《我是歌手》
C. 射击运动员射击一次,命中十环 D. 方程x2-2x-1=0必有实数根
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若等腰三角形的周长为17cm,其中一边长为7cm,则该等腰三角形的底边长为( )
A. 3cm B. 3cm或5cm C. 3cm或7cm D. 7cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com