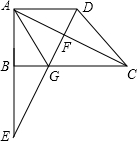
解:(1)BF=x=4时,AE=6-2=4=BF,
∵∠A=∠B=90°,菱形EFGH,
∴EH=EF,
∵在Rt△AEH和Rt△BFE中

,
∴Rt△AEH≌Rt△BFE,
∴∠AEH=∠EFB,
∵∠BEF+∠EFB=90°,
∴∠AEH+∠BEF=90°,
∴∠HEF=180°-90°=90°,
即菱形EFGH是正方形
∴当x=4时,四边形FEHG为正方形;
(2)如图,连接FH,作GQ⊥BC于Q,则∠GQF=90°,∠GQF=∠A.
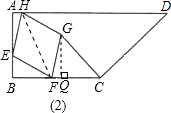
∵菱形FEHG,
∴GF=EH,EH∥FG,
∴∠EHF=∠GFH,
∵直角梯形ABCD中,AD∥BC,
∴∠AHF=∠HFC,
∴∠AHF-∠EHF=∠HFC-∠GFH,即∠AHE=∠GFQ,
∴△QGF≌△AEH,
∴GQ=EA=AB-BE=4,
∵BC=8,BF=x,
∴S
△FCG=

×CF×GQ=16-2x.
∴y与x的函数关系式y=16-2x;
(3)①如图,
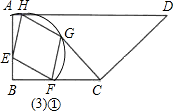
当点F运动到使菱形FEHG的顶点H与点A重合时,x取得最小值,△FCG的面积最大,
画法如下:以E为圆心,EA为半径画弧,交BC边上于点F,平移EA到FG,连接AG,得到四边形FEHG为菱形,此时EF=EA=AB-BE=4,BF=
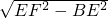
=

=2

.
y=16-2x=16-4

,
△FCG的面积的最大值为16-4

.
②如图,
当点F运动到使菱形FEHG的顶点G落在梯形ABCD的CD边上时,x取最大值,△FCG的面积取得最小值,画法如下:在图6中有GQ=4可知.无论点F在BC边上如何运动,点G到BC及AD的距离都不变,分别为4、2,取AE的中点P,(AP=2),过点P作BC的平行线,交CD与G,作EG的垂直平分线,分别交AD、BC于H、F,顺次连接F、E、H、G得到四边形FEHG,可证的四边形FEHG为菱形.
如图,作CM⊥AD与M,GK⊥AD于K,则BP=4,EP=AP=2,
∵梯形ABCD中,AB=6,BC=8.AD=14,

∴CM=AB=6,DM=AD-AM=6,GK=AP=2,
∵DM=CM,∠CMD=90°,
∴∠D=45°,
∴DK=GK=2,PG=AK=AD-DK=12,
与(2)同理可证△KGH≌△BEF,KH=BF,
设此时的BF=x,则AH=AD-KH-DK=14-BF-2=12-x,在直角三角形AEH与直角三角形BEF中,由勾股定理得
AE
2+AH
2=EH
2,BE
2+BF
2=EF
2,由菱形的性质可知EH=EF,
∴AE
2+AH
2=BE
2+BF
2,即4
2+(12-x)
2=2
2+x
2,解得x=

,此时y=16-2x=3,
∴△FCG面积的最小值为3;
(4)答:△FCG面积由最大值变到最小值时,点G运动的路线长为12-2

.
分析:(1)根据直角梯形ABCD中,AD∥BC,∠A=90°,AB=6,BC=8,AD=14可直接求出答案;
(2)连接FH,作GQ⊥BC于Q,根据菱形FEHG,求证△QGF≌△AEH,可得S
△FCG=

×CF×GQ=16-2x,然后即可求得y与x的函数关系式;
(3)当点F运动到使菱形FEHG的顶点H与点A重合时,x取得最小值,△FCG的面积最大,利用勾股定理求得BF,可得y=16-2x=16-4

,然后即可求得△FCG的面积的最大值;
(4)如下图,在题图的基础上,继续作CM⊥AD与M,GK⊥AD于K,由(3)求得的△FCG的面积的最大值和△FCG面积的最小值为3,即可直接得出答案.
点评:此题主要考查直角梯形,全等三角形的判定与性质,勾股定理,正方形的性质等知识点的理解和掌握,此题有一定的拔高难度,属于难题.

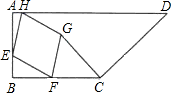 形ABCD内或其边上.若BF=x,△FCG的面积为y.
形ABCD内或其边上.若BF=x,△FCG的面积为y. ,
,
 ×CF×GQ=16-2x.
×CF×GQ=16-2x.
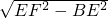 =
= =2
=2 .
. ,
, .
.
 ,此时y=16-2x=3,
,此时y=16-2x=3, .
. ×CF×GQ=16-2x,然后即可求得y与x的函数关系式;
×CF×GQ=16-2x,然后即可求得y与x的函数关系式; ,然后即可求得△FCG的面积的最大值;
,然后即可求得△FCG的面积的最大值;

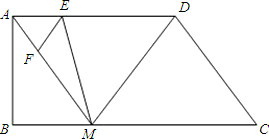 、F分别是线段AD、AM上的动点(点E与A、D不重合)且∠FEM=∠AMB,设DE=x,MF=y.
、F分别是线段AD、AM上的动点(点E与A、D不重合)且∠FEM=∠AMB,设DE=x,MF=y.