
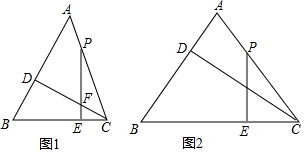
分析 (1)结论:PF=2CE.由△PCE∽△BCD∽△CEF,得$\frac{PE}{CD}$=$\frac{CE}{BD}$,$\frac{EF}{BD}$=$\frac{CE}{CD}$,即$\frac{PE}{CE}$=$\frac{CD}{BD}$①,$\frac{EF}{CE}$=$\frac{BD}{CD}$②,①-②得$\frac{PE-EF}{CE}$=$\frac{CD}{BD}$-$\frac{BD}{CD}$,由PE-EF=PF,可得$\frac{PF}{CE}$=$\frac{CD}{BD}$-$\frac{BD}{CD}$,设CD=a,则AD=a,AC=AB=$\sqrt{2}$a,推出BD=AB-AD=($\sqrt{2}$-1)a,可得$\frac{PF}{CE}$=$\frac{a}{(\sqrt{2}-1)a}$-$\frac{(\sqrt{2}-1)a}{a}$=2.
(2)结论:$\frac{PF}{CE}$=2k.由(1)知:△PCE∽△BCD∽△CEF,同理可得:$\frac{PF}{CE}$=$\frac{CD}{BD}$-$\frac{BD}{CD}$,设CD=b,则AD=kb,AC=AB=$\sqrt{1+{k}^{2}}$b,推出BD=AB-AD=($\sqrt{1+{k}^{2}}$-k)b,可得$\frac{PF}{CE}$=$\frac{b}{(\sqrt{1+{k}^{2}}-k)b}$-$\frac{(\sqrt{1+{k}^{2}}-k)b}{b}$═2k.
解答 解:(1)结论:PF=2CE.理由如下,
∵CD是AB边上的高,PE⊥BC
∴∠BDC=∠PEC=90°
∴∠DCB=90°-∠B,∠CPE=90°-∠ACB
∵AB=AC
∴∠DCB=∠CPE
∴△PCE∽△BCD∽△CEF
∴$\frac{PE}{CD}$=$\frac{CE}{BD}$,$\frac{EF}{BD}$=$\frac{CE}{CD}$,即$\frac{PE}{CE}$=$\frac{CD}{BD}$①,$\frac{EF}{CE}$=$\frac{BD}{CD}$②
①-②得$\frac{PE-EF}{CE}$=$\frac{CD}{BD}$-$\frac{BD}{CD}$,
∵PE-EF=PF
∴$\frac{PF}{CE}$=$\frac{CD}{BD}$-$\frac{BD}{CD}$,
设CD=a,则AD=a,AC=AB=$\sqrt{2}$a
∴BD=AB-AD=($\sqrt{2}$-1)a
∴$\frac{PF}{CE}$=$\frac{a}{(\sqrt{2}-1)a}$-$\frac{(\sqrt{2}-1)a}{a}$=2,
∴PF=2CE
(2)结论:$\frac{PF}{CE}$=2k.理由如下,
如图2,由(1)知:△PCE∽△BCD∽△CEF,
同理可得:$\frac{PF}{CE}$=$\frac{CD}{BD}$-$\frac{BD}{CD}$,
设CD=b,则AD=kb,AC=AB=$\sqrt{1+{k}^{2}}$b
∴BD=AB-AD=($\sqrt{1+{k}^{2}}$-k)b
∴$\frac{PF}{CE}$=$\frac{b}{(\sqrt{1+{k}^{2}}-k)b}$-$\frac{(\sqrt{1+{k}^{2}}-k)b}{b}$═2k.
点评 本题考查相似三角形的判定和性质、等腰三角形的性质等知识,解题的关键是熟练应用相似三角形的性质解决问题,学会利用参数解决问题,属于中考压轴题.


科目:初中数学 来源: 题型:解答题
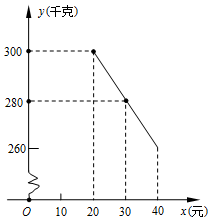 草莓是云南多地盛产的一种水果,今年某水果销售店在草莓销售旺季,试销售成本为每千克20元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克40元,经试销发现,销售量y(千克)与销售单价x(元)符合一次函数关系,如图是y与x的函数关系图象.
草莓是云南多地盛产的一种水果,今年某水果销售店在草莓销售旺季,试销售成本为每千克20元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克40元,经试销发现,销售量y(千克)与销售单价x(元)符合一次函数关系,如图是y与x的函数关系图象.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
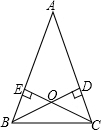 如图,在△ABC中,AB=AC,BD、CE是腰AB、AC上的高,交于点O.
如图,在△ABC中,AB=AC,BD、CE是腰AB、AC上的高,交于点O.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com