
 如图,已知△ABC的周长为24,OB,OC分别平分∠ABC,∠ACB,OD⊥BC于点D,且OD=2,求△ABC的面积.
如图,已知△ABC的周长为24,OB,OC分别平分∠ABC,∠ACB,OD⊥BC于点D,且OD=2,求△ABC的面积. 分析 连接OA,作OE⊥AB于E,OF⊥AC与F,根据角平分线的性质求出OE、OF的长,根据△ABC的面积=△A0B的面积+△BOC的面积+△AOC的面积计算即可.
解答  解:连接OA,作OE⊥AB于E,OF⊥AC与F,
解:连接OA,作OE⊥AB于E,OF⊥AC与F,
∵OB,OC分别平分∠ABC,∠ACB,OD⊥BC,OE⊥AB,OF⊥AC,
∴OE=OE=OD=2,
△ABC的面积=△A0B的面积+△BOC的面积+△AOC的面积
=$\frac{1}{2}$AB•OE+$\frac{1}{2}$AC•OF+$\frac{1}{2}$CB•OD
=$\frac{1}{2}$×(AB+AC+BC)×2
=24.
答:△ABC的面积是24.
点评 本题主要考查平分线的性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键,注意辅助线的作法要正确.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题:
正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x | … | -6 | -5 | -4 | -3 | -2 | -1 | 1 | 2 | 3 | 4 | 5 | 6 | … |
| $y=\frac{6}{x}$ | … | -1 | -1.5 | -2 | 6 | 3 | 2 | 1.2 | 1 | … |

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
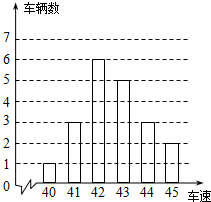 已知:如图,是交警在某个路口统计的某时段来往车辆的车速(单位:千米/时)情况.
已知:如图,是交警在某个路口统计的某时段来往车辆的车速(单位:千米/时)情况.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com