
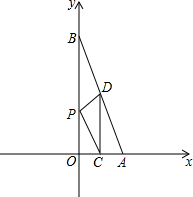
 如图,一次函数y=kx+b的图象与x,y轴分别交于A(2,0)和B(0,8)点C,D分别在OA,AB上,且C(1,0),D(1,m).
如图,一次函数y=kx+b的图象与x,y轴分别交于A(2,0)和B(0,8)点C,D分别在OA,AB上,且C(1,0),D(1,m).分析 (1)利用待定系数法求出函数解析式,代入法求出m的值,即可解答;
(2)设点C关于点O的对称点为C′,连接C′D交OB于P,则PC=PC′,PC+PD=PC′+PD=C′D,即PC+PD的最小值是C′D.连接CD,在Rt△DCC′中,由勾股定理求得C′D的值,即可解答;
(3)△PCD为等腰三角形时,分三种情况讨论:
①当PC=PD时,P在CD的垂直平分线上,与y轴交点即为点P;
②当CP=CD时,CP=2,以C为圆心,2为半径画弧,与y轴交于两点;
③当DP=CD时,以D为圆心,2为半径画弧,与y轴交于两点;共5个解.
解答 解:(1)把A(2,0)和B(0,8)代入一次函数y=kx+b得:
$\left\{\begin{array}{l}{2k+b=0}\\{b=8}\end{array}\right.$
解得:$\left\{\begin{array}{l}{k=-4}\\{b=8}\end{array}\right.$
则一次函数解析式为y=-4x+8,
把D(1,m)代入y=-4x+8得:
m=-4+8=4.
(2)如图1,
∵点C的坐标为(1,0),
则C关于y轴的对称点为C′(-1,0),
又∵点D的坐标为(1,4),
连接C′D,设C′D的解析式为y=kx+b,
有$\left\{\begin{array}{l}{-k+b=0}\\{k+b=4}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=2}\\{b=2}\end{array}\right.$,
∴y=2x+2是DC′的解析式,
∵x=0,∴y=2,
即P(0,2).
∵PC+PD的最小值=C′D,
∴CD=3,CC′=2,
由勾股定理得C′D=$\sqrt{{3}^{2}+{2}^{2}}=\sqrt{13}$.
(3)△PCD为等腰三角形时,分三种情况讨论:
①当PC=PD时,P在CD的垂直平分线上,与y轴交点即为点P,坐标为(0,2);
②当CP=CD时,CP=4,以C为圆心,4为半径画弧,与y轴交于两点,坐标分别为(0,$\sqrt{15}$),(0,-$\sqrt{15}$);
③当DP=CD时,以D为圆心,4为半径画弧,与y轴交于两点,坐标分别为(0,4+$\sqrt{15}$),(0,4-$\sqrt{15}$);
综上所述:当△PCD为等腰三角形时,点P坐标为(0,1)或(0,$\sqrt{15}$),或(0,-$\sqrt{15}$),或(0,4+$\sqrt{15}$),或(0,4-$\sqrt{15}$)
点评 本题考查了一次函数的综合应用及最短路线问题,用到的知识点是待定系数法求一次函数的解析式,两点之间线段最短的定理以及勾股定理的运用,本题有一定的难度,注意第(3)问点P有五种情况,不要漏项.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 已知:△ABD和△CBD关于直线BD对称(点A的对称点是点C),点E,F分别是线段BC和线段BD上的点,且点F在线段EC的垂直平分线上,连接AF,AE,AE交BD于点G.如图,求证:∠EAF=∠ABD.
已知:△ABD和△CBD关于直线BD对称(点A的对称点是点C),点E,F分别是线段BC和线段BD上的点,且点F在线段EC的垂直平分线上,连接AF,AE,AE交BD于点G.如图,求证:∠EAF=∠ABD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com