
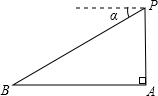
 如图,飞机P在目标A的正上方1100m处,飞行员测得地面目标B的俯角α=30°,求地面目标A、B之间的距离(精确到个位).
如图,飞机P在目标A的正上方1100m处,飞行员测得地面目标B的俯角α=30°,求地面目标A、B之间的距离(精确到个位).  英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案科目:初中数学 来源: 题型:
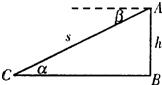 11、如图,飞机A在目标B的正上方,在地面C处测得飞机的仰角为α,在飞机上测得地面C处的俯角为β,飞行高度为h,AC间距离为s,从这4个已知量中任取2个为一组,共有6组,那么可以求出BC间距离的有( )
11、如图,飞机A在目标B的正上方,在地面C处测得飞机的仰角为α,在飞机上测得地面C处的俯角为β,飞行高度为h,AC间距离为s,从这4个已知量中任取2个为一组,共有6组,那么可以求出BC间距离的有( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com