
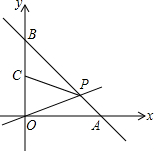
 已知一次函数y=kx-2k+3(k<0)的图象与x轴交于点A,与y轴交于点B.
已知一次函数y=kx-2k+3(k<0)的图象与x轴交于点A,与y轴交于点B.分析 (1)根据y=kx-2k+3=y=k(x-2)+3,可得当x=2时,y=3,所以无论k(k<0)为何值时,直线AB都经过一定点(2,3),即点H的坐标是(2,3).
(2)首先根据k=-1,可得y=kx-2k+3=-x+5,再联立y=mx,求出点P的坐标是多少,进而求出PC所在直线的斜率的值是多少;然后根据∠CPO=45°,求出m的值是多少即可.
(3)首先根据点到直线的距离的求法,求出d的值是多少;然后根据k<0,方程有负实数解,求出d的最小值是多少即可.
解答 解:(1)∵y=kx-2k+3=y=k(x-2)+3,
∴当x=2时,y=3,
∴点H的坐标是(2,3).
(2)当k=-1时,
y=kx-2k+3=-x+5,
联立$\left\{\begin{array}{l}{y=-x+5}\\{y=mx}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=\frac{5}{m+1}}\\{y=\frac{5m}{m+1}}\end{array}\right.$,
即点P的坐标是($\frac{5}{m+1},\frac{5m}{m+1}$),
∴PC所在直线的斜率是:
$\frac{\frac{5m}{m+1}-\frac{13}{5}}{\frac{5}{m+1}-0}$=$\frac{12m-13}{25}$
∵∠CPO=45°,
∴tan45°=$\frac{m-\frac{12m-13}{25}}{1+m×\frac{12m-13}{25}}$
=$\frac{13m+13}{1{2m}^{2}-13m+25}$
=1
∴6m2-13m+6=0,
解得m=$\frac{2}{3}$或m=$\frac{3}{2}$.
(3)∵y=kx-2k+3,
∴d=$\frac{|3-2k|}{\sqrt{{k}^{2}+1}}=\frac{3-2k}{\sqrt{{k}^{2}+1}}$,
∴d2(k2+1)=(3-2k)2,
∴(d2-4)k2+12k+d2-9=0,
∵k<0,方程有负实数解,
∴$\left\{\begin{array}{l}{{12}^{2}-4{(d}^{2}-4){(d}^{2}-9)≥0}\\{-\frac{12}{2{(d}^{2}-4)}<0}\\{{d}^{2}-9≥0}\end{array}\right.$
整理,可得
9≤d2≤13,
∴d的最小值是3.
点评 (1)此题主要考查了一次函数综合题,考查了分析推理能力,考查了从已知函数图象中获取信息,并能利用获取的信息解答相应的问题的能力.
(2)此题还考查了点的坐标的含义以及求法,以及两条直线的夹角的性质的应用,要熟练掌握.
(3)此题还考查了点到直线的距离公式,要熟练掌握.


科目:初中数学 来源: 题型:选择题
 如图,⊙O为△PEF的内切圆,A,B,D为切点,DE=DF,C为弧$\widehat{ADB}$上一点,若AE=10,则EF的长为( )
如图,⊙O为△PEF的内切圆,A,B,D为切点,DE=DF,C为弧$\widehat{ADB}$上一点,若AE=10,则EF的长为( )| A. | 4$\sqrt{5}$ | B. | 3$\sqrt{5}$ | C. | 20 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,∠ABC=90°,以AB的中点O为圆心,OA为半径的圆交AC于点D,E是BC的中点,连结DE、OE.
如图,在△ABC中,∠ABC=90°,以AB的中点O为圆心,OA为半径的圆交AC于点D,E是BC的中点,连结DE、OE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点N(0,6),点M在x轴负半轴上,ON=3OM,A为线段MN上一点,AB⊥x轴,垂足为B,AC⊥y轴,垂足为C,AB=$\frac{1}{3}$ON.
如图,点N(0,6),点M在x轴负半轴上,ON=3OM,A为线段MN上一点,AB⊥x轴,垂足为B,AC⊥y轴,垂足为C,AB=$\frac{1}{3}$ON.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 业务种类 | 计费单位 | 资费标准/元 | |
| 本埠资费 | 外埠资费 | ||
| 信函 | 首重100克内,每重20克(不足20克按20克计算) | 0.80 | 1.20 |
| 续重101-2000克每重100克(不足100克按100克计算) | 1.20 | 2.00 | |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
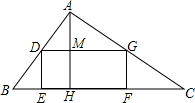 如图,矩形DEFG内接于Rt△ABC,∠BAC=90°,AH是斜边上的高,BH=1,AH=2.
如图,矩形DEFG内接于Rt△ABC,∠BAC=90°,AH是斜边上的高,BH=1,AH=2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com