
【题目】如图,OB,AB表示甲、乙两名同学运动的一次函数图象,图中s和t分别表示运动路程和时间,已知甲的速度比乙快,下列说法:①射线AB表示甲的路程与时间的函数关系;②甲的速度比乙快1.5 m/s;③乙在甲前面12 m处起跑;④ 8 s后,甲超过了乙.其中正确的说法是( )
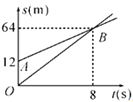
A. ①② B. ②③④ C. ②③ D. ①③④
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】在学习三角形中位线的性质时,小亮对课本给出的解决办法进行了认真思考: 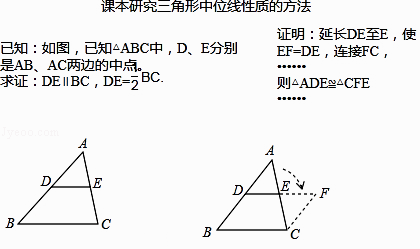 请你利用小亮的发现解决下列问题:
请你利用小亮的发现解决下列问题:
(1)如图1,AD是△ABC的中线,BE交AC于E,交AD于E,且AE=EF,求证:AC=BF. 请你帮助小亮写出辅助线作法并完成论证过程: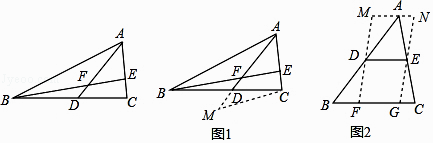
(2)解决问题:如图2,在△ABC中,∠B=45°,AB=10,BC=8,DE是△ABC的中位线,过点D、E作DF∥EG,分别交BC于F、G,过点A作MN∥BC,分别与FE、GE的延长线交于M、N,则四边形MFGN周长的最小值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小张同学在计算![]() 时,将“
时,将“![]() ”错看成了“
”错看成了“![]() ”,得出的结果是
”,得出的结果是![]() .
.
(1)请你求出这道题的正确结果;
(2)试探索:当字母![]() 、
、![]() 满足什么关系时,(1)中的结果与字母
满足什么关系时,(1)中的结果与字母![]() 的取值无关.
的取值无关.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列一元一次方程解应用题.
(1)商店出售茶壶和茶杯,茶壶每只定价20元,茶杯每只定价5元,该商品制定了两种优惠方法:
①买一只茶壶赠一只茶杯;②按总价的90%付款.某顾客购买茶壶5只,茶杯若干只(不少于5只),问顾客买多少只茶杯时,两种方法付款相同.假如该顾客买了茶杯20只,哪种买法实惠?
(2)某人原计划骑车以每小时12千米的速度由A地到B地,这样便可在规定的时间到达,但他因事将原计划出发的时间推迟了20分钟,只好以每小时15千米的速度前进,结果比规定时间早4分钟到达B地,求A,B两地间的距离.
(3)某工厂完成一批产品,一车间单独完成需30天,二车间单独完成需20天.
①如一车间先做若干天,然后由二车间继续做,直至完成,前后共做了25天,问一车间先做了几天?
②如一车间先做了3天后,二车间加入一起做,还需多少天才能完成?
查看答案和解析>>
科目:初中数学 来源: 题型:
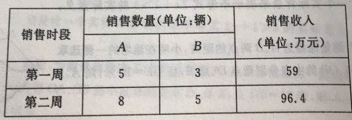
【题目】2017年12月29日郑州市人民政府通告:为减少机动车污染物排放,持续改善我市空气质量,从2018年1月1日起,每周工作日的7时至21时郑州市东三环、南三环、西三环、北三环以内区域的所有道路限行按机动车号牌(含临时号牌和外地号牌)最后一位阿拉伯数字(尾数为字母的以末尾数字为准),工作日每天限行2个号,即:号码最后一位阿拉伯数字为1和6的机动车周一限行,2和7的机动车周二限行,3和8的机动车周三限4和9的机动车周四限行,5和0的机动车周五限行,因法定节假日放假、调休而调整为上班的周六、周日按对应调体的工作日限行但通告中还规定,悬挂新能源专用牌的新能源汽车不受限制.限行通告发布后,新能源汽车成为畅销车型,某4S店销售每辆进价分别为5万元、9万元的A、B两种型号的新能源汽车,下表是近两周的销售情况:
(1)求A、B两种型号的新能源汽车的销售单价;(共
(2)若4S店准备用不超过200万元的金额采购这两种型号的新能源汽车共30辆,求B型号的新能源汽车最多能采购多少辆?
(进价、售价均保持不变,利润=销售收入一进货成本)
(3在(2)的条件下,4S销售完这230辆新能源汽车时45店的最大利润是多少?并写
查看答案和解析>>
科目:初中数学 来源: 题型:
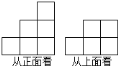
【题目】由若干个(大于![]() 个)大小相同的正方体组成一个几何体的从正面看和从上面看如图所示,则这个几何体的从左面看不可能是下列图中的( )
个)大小相同的正方体组成一个几何体的从正面看和从上面看如图所示,则这个几何体的从左面看不可能是下列图中的( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是放在地面上的一个长方体盒子,其中AB=18cm,BC=12cm,BF=10cm,点M在棱AB上,且AM=6cm,点N是FG的中点,一只蚂蚁要沿着长方体盒子的表面从点M爬行到点N,它需要爬行的最短路程为____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在东西方向的海岸线l上有一长为1千米的码头MN,在码头西端M的正西方向30 千米处有一观察站O.某时刻测得一艘匀速直线航行的轮船位于O的北偏西30°方向,且与O相距 ![]() 千米的A处;经过40分钟,又测得该轮船位于O的正北方向,且与O相距20千米的B处.
千米的A处;经过40分钟,又测得该轮船位于O的正北方向,且与O相距20千米的B处.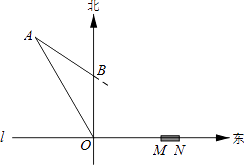
(1)求该轮船航行的速度;
(2)如果该轮船不改变航向继续航行,那么轮船能否正好行至码头MN靠岸?请说明理由.(参考数据: ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
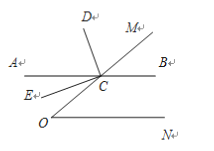
【题目】已知:如图,点C在∠MON的一边OM上,过点C的直线AB∥ON,CD平分∠ACM,CE⊥CD.
(1)若∠O=50°,求∠BCD的度数;
(2)求证:CE平分∠OCA;
(3)当∠O为多少度时,CA分∠OCD成1:2两部分,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com