
 如图,△AOB中,∠AOB=90°,AO=3OB,反比例函数y=$\frac{9}{x}$(x>0)的图象经过点A,把△AOB沿直线OA翻折,点B的对应点为点B′.若反比例函数y=$\frac{k}{x}$(x>0)的图象经过点B′,则k的值为( )
如图,△AOB中,∠AOB=90°,AO=3OB,反比例函数y=$\frac{9}{x}$(x>0)的图象经过点A,把△AOB沿直线OA翻折,点B的对应点为点B′.若反比例函数y=$\frac{k}{x}$(x>0)的图象经过点B′,则k的值为( )| A. | 3 | B. | -3 | C. | 1 | D. | -1 |
分析 过点A作AE⊥x轴于点E,过点B作BF⊥x轴于点F,则△BOF∽△OAE,由点A在反比例函数y=$\frac{9}{x}$(x>0)的图象上可知AE•OE=9OF•BF=9,设点B′的坐标为(m,$\frac{k}{m}$),根据点B和点B′关于OA对称即可得出m=OF、$\frac{k}{m}$=-BF,二者相乘即可得出k值.
解答 解:过点A作AE⊥x轴于点E,过点B作BF⊥x轴于点F,如图所示.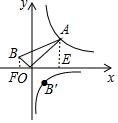
∵∠AOB=90°,
∴∠AOE+∠BOF=90°,
∵∠AOE+∠OAE=90°,
∴∠BOF=∠OAE.
∵∠BFO=∠OEA=90°,
∴△BOF∽△OAE.
∵AO=3OB,反比例函数y=$\frac{9}{x}$(x>0)的图象经过点A,
∴AE•OE=9OF•BF=9.
设点B′的坐标为(m,$\frac{k}{m}$),
∴m=OF,$\frac{k}{m}$=-BF,
∴k=m•$\frac{k}{m}$=-OF•BF=-1.
故选D.
点评 本题考查了反比例函数图象上点的坐标特征、相似三角形的判定与性质以及翻折变换,利用相似三角形的性质找出AE•OE=9OF•BF=9是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| A | B | |
| 载客量(人/辆) | 40 | 20 |
| 租金(元/辆) | 200 | 150 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
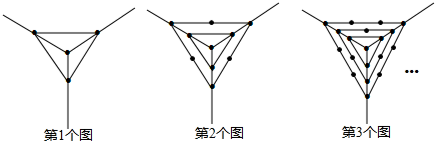
| A. | 38 | B. | 46 | C. | 61 | D. | 64 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com