分析 首先根据题意列出表格，然后由表格即可求得所有等可能的结果与两次摸到相同颜色的球情况，再利用概率公式即可求得答案．
解答 解：列表得：
第二次 第一次 | 红球1 | 红球2 | 红球3 | 白球1 | 白球2 |
| 红球1 | （红1，红1） | （红1，红2） | （红3，红1） | （红1，白1） | （红1，白2） |
| 红球2 | （红2，红1） | （红2，红2） | （红3，红2） | （红2，白1） | （红2，白2） |
| 红球3 | （红3，红1） | （红3，红2） | （红3，红3） | （红3，白1） | （红3，白2） |
| 白球1 | （白1，红1） | （白1，红2） | （红3，白1） | （白1，白1） | （白1，白2） |
| 白球2 | （白2，红1） | （白2，红2） | （红3，白2） | （白2，白1） | （白2，白2） |
点评 此题考查的是用列表法或树状图法求概率．列表法可以不重复不遗漏的列出所有可能的结果，适合于两步完成的事件；树状图法适合两步或两步以上完成的事件；解题时要注意此题是放回实验还是不放回实验．用到的知识点为：概率=所求情况数与总情况数之比．
天天向上口算本系列答案科目：初中数学 来源： 题型：选择题
| A． | $\frac{1}{4}$ | B． | $\frac{\sqrt{2}}{4}$ | C． | $\frac{3}{4}$ | D． | $\frac{\sqrt{3}}{4}$ |
查看答案和解析>>
科目：初中数学 来源： 题型：填空题
如图，二次函数y=ax2+bx+c的图象经过点（-1，2），且与x轴交点的横坐标分别为x1，x2，其中-2＜x1＜-1，0＜x2＜1．下列结论：①4a-2b+c＜0；②2a-b＜0；③b＜1；④a＞-$\frac{1}{2}$；⑤（a+c）2＜b2中正确的有①②⑤（将你认为正确的结论番号都填出来）查看答案和解析>>
科目：初中数学 来源： 题型：解答题
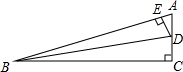如图，在Rt△ABC中，∠C=90°，点D，E分别在边AC，AB上，BD是∠ABC的平分线，DE⊥AB，AE=10，cosA=$\frac{5}{13}$．查看答案和解析>>
科目：初中数学 来源： 题型：选择题
已知抛物线y=$\frac{1}{2}$（x-3）2-2的部分图象（如图），图象再次与x轴相交时的坐标是（ ）| A． | （2，0） | B． | （3，0） | C． | （4，0） | D． | （5，0） |
查看答案和解析>>
科目：初中数学 来源： 题型：解答题
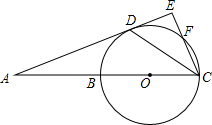如图，直线AD切⊙O于点D，直线AB经过圆心O，交⊙O于点B、C，CE⊥AD，垂足为E，CE交⊙O于点F，连接CD．查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
如图，已知AC、BD相交于O，AE=FC，AO=OC，BO=OD．求证：∠1=∠2．
如图，在正方体的两个面上画了两条对角线AB，AC，则∠BAC等于（ ）