
已知:正方形ABCD的边长为6,点E为BC的中点,点F在AB边上,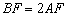 .
.
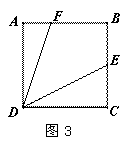
画出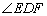 ,猜想
,猜想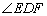 的度数并写出计算过程.
的度数并写出计算过程.
解: 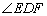 的度数为 .
的度数为 .
计算过程如下:
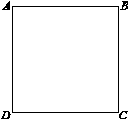
解:所画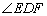 如图3所示.
如图3所示.
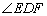 的度数为
的度数为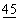 .
.
解法一:如图4,连接EF,作FG⊥DE于点G.
∵ 正方形ABCD的边长为6,
∴ AB=BC=CD= AD =6,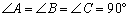 .
.
∵ 点E为BC的中点,
∴ BE=EC=3.
∵ 点F在AB边上,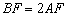 ,
,
∴ AF=2,BF=4.
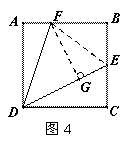
在Rt△ADF中,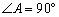 ,
,
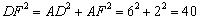 .
.
在Rt△BEF,Rt△CDE中,同理有
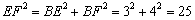 ,
,
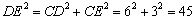 .
.
在Rt△DFG和Rt△EFG中,有 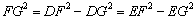 .
.
设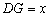 ,则
,则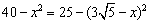 .
.
整理,得 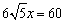 .
.
解得 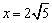 ,即
,即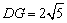 .
.
∴ 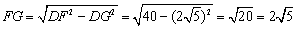 .
.
∴ 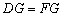 .
.
∵ 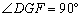 ,
,
∴ 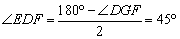 .
.
解法二:如图5,延长BC到点H,使CH=AF,连接DH,EF.
∵ 正方形ABCD的边长为6,
∴ AB=BC=CD=AD =6,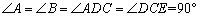 .
.
∴ 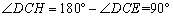 ,
,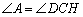 .
.
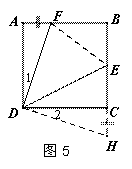 在△ADF和△CDH中,
在△ADF和△CDH中,
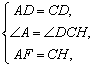
∴ △ADF≌△CDH.(SAS)
∴ DF=DH, ①
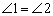 .
.
∴ 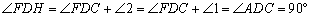
∵ 点E为BC的中点,
∴ BE=EC=3.
∵ 点F在AB边上,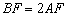 ,
,
∴ CH= AF=2,BF=4.
∴ 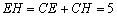 .
.
在Rt△BEF中,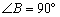 ,
,
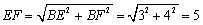 .
.
∴ 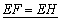 .②
.②
又∵ DE= DE,③
由①②③得△DEF≌△DEH.(SSS)
∴ 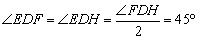 .
.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
已知:在平面直角坐标系xOy中,一次函数 的图象与y轴交于点A,与x
的图象与y轴交于点A,与x
轴的正半轴交于点B, .
.
(1)求点A、点B的坐标;(2)求一次函数的解析式.
解:

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,菱形ABCD的边长为48cm,∠A=60°,动点P从点A出发,沿着线路AB—BD做匀速运动,动点Q从点D同时出发,沿着线路DC-CB-BA做匀速运动.
 |
(1)求BD的长;
(2)已知动点P、Q运动的速度分别为8cm/s、10cm/s.经过
12秒后 ,P、Q分别到达M、N两点,试判断△AMN的
,P、Q分别到达M、N两点,试判断△AMN的
形状,并说明理由,同时求出△AMN的面积;
(3)设问题(2)中的动点P、Q分别从M、N同时沿原路返回,
动点P的速度不变,动点Q的速度改变为a cm/s,经过3秒后,P、Q分别到达E、F两点,若△BEF为直角三角形,试求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com