
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
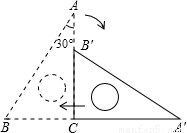
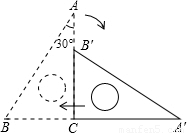
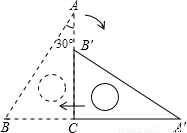
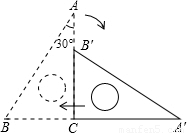
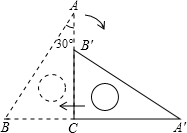 如图,斜边长为6cm,∠A=30°的直角三角板ABC绕点C顺时针方向旋转90°至△A′B′C的位置,再沿CB向左平移使点B′落在原三角板ABC的斜边AB上.则三角板向左平移的距离为
如图,斜边长为6cm,∠A=30°的直角三角板ABC绕点C顺时针方向旋转90°至△A′B′C的位置,再沿CB向左平移使点B′落在原三角板ABC的斜边AB上.则三角板向左平移的距离为查看答案和解析>>
科目:初中数学 来源:第27章《相似》中考题集(11):27.2 相似三角形(解析版) 题型:填空题
查看答案和解析>>
科目:初中数学 来源:第29章《相似形》常考题集(09):29.5 相似三角形的性质(解析版) 题型:填空题
查看答案和解析>>
科目:初中数学 来源:第4章《相似三角形》常考题集(03):4.2 相似三角形(解析版) 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com