
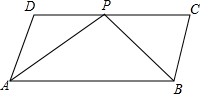
 如图,ABCD是平行四边形,P是CD上一点,且AP和BP分别平分∠DAB和∠CBA.
如图,ABCD是平行四边形,P是CD上一点,且AP和BP分别平分∠DAB和∠CBA.分析 (1)根据平行四边形性质得出AD∥CB,AB∥CD,推出∠DAB+∠CBA=180°,求出∠PAB+∠PBA=90°,在△APB中求出∠APB即可;
(2)求出AD=DP=5,BC=PC=5,求出DC=10=AB,即可求出答案.
解答 证明:(1)∵ABCD是平行四边形,
∴AD∥CB.∴∠DAB+∠CBA=180°.
又∵AP和BP分别平分∠DAB和∠CBA,
∴∠PAB+∠PBA=$\frac{1}{2}$(∠DAB+∠CBA)=90°.
在△APB中,∵∠APB=180°-(∠PAB+∠PBA)=90°.
∴AP⊥PB;
(2)∵AP平分∠DAB且AB∥CD,
∴∠DAP=∠PAB=∠DPA.
∴△ADP是等腰三角形.
∴AD=DP=5cm.
同理,PC=CB=5cm.
∴AB=DP+PC=10cm.
在Rt△APB中,AB=10cm,AP=8cm,
∴BP=$\sqrt{1{0}^{2}-{8}^{2}}$=6(cm).
∴△APB的周长是6+8+10=24(cm).
点评 本题考查了平行四边形性质,平行线性质,等腰三角形的性质和判定,三角形的内角和定理,勾股定理等知识点的综合运用.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
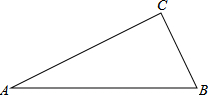 如图,在Rt△ABC中,∠C=90°,
如图,在Rt△ABC中,∠C=90°,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com