
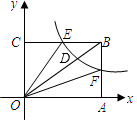
 ��ͼ���ھ���OABC�У�F��AB�ϵ�һ�����㣨F����A��B�غϣ�������F�ķ���������y=$\frac{k}{x}$��ͼ����BC�߽��ڵ�E��
��ͼ���ھ���OABC�У�F��AB�ϵ�һ�����㣨F����A��B�غϣ�������F�ķ���������y=$\frac{k}{x}$��ͼ����BC�߽��ڵ�E������ ��1���ֱ����E��F�����꣬�Ӷ��ɱ�ʾ��B�����꣬����S����OABC-S��OCE-S��OAF=6�õ�����k�ķ��̣�����ú�������ʽ��
��2����D��DM��OA�ڵ�M�������������D�����꣬����ƽ���߷��߶γɱ��������OA��AB�ij����Ӷ������B�����ꣻ
��3����k�ɷֱ��ʾ��E��F�����꣬�Ӷ��ɱ�ʾ����EFA������������ö��κ��������ʿ���������ֵ��
��� �⣺
��1���ھ���OABC�У����E����Ϊ��a��b������F����Ϊ��x��y�������B����Ϊ��x��2y����
��${S_{��OCE}}=\frac{1}{2}ab=\frac{1}{2}k$��${S_{��OAF}}=\frac{1}{2}xy=\frac{1}{2}k$��S����OABC=2xy=2k��
��S����OABC-S��OCE-S��OAF=6��
��$2k-\frac{1}{2}k-\frac{1}{2}k=6$�����k=6��
��ú����Ľ���ʽΪy=$\frac{6}{x}$��
��2������D����DM��OA�ڵ�M����ͼ1��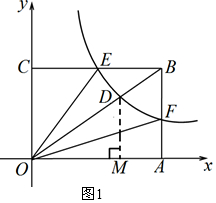
�������֪D�������Ϊ$x=2\sqrt{2}$����������$y=\frac{6}{{2\sqrt{2}}}=\frac{{3\sqrt{2}}}{2}$��
��DM��BA��
��$\frac{OM}{OA}=\frac{DM}{BA}=\frac{OD}{OB}=\frac{{\sqrt{2}}}{2}$����$\frac{2\sqrt{2}}{OA}$=$\frac{\sqrt{2}}{2}$�����OA=4��$\frac{\frac{3\sqrt{2}}{2}}{BA}$=$\frac{\sqrt{2}}{2}$�����AB=3��
���B������4��3����
��3��E��F��������ֱ�ΪE��$\frac{k}{3}$��3����F��4��$\frac{k}{4}$����
��S��EFA=$\frac{1}{2}$AF•BE=$\frac{1}{2}$��$\frac{k}{4}$��4-$\frac{k}{3}$��=-$\frac{1}{24}$k2+$\frac{1}{2}$k=-$\frac{1}{24}$��k-6��2+$\frac{3}{2}$��
��-$\frac{1}{24}$��0��
�൱k=6ʱ��S�����ֵ��S���ֵ=$\frac{3}{2}$��
���� ����Ϊ�������������ۺ�Ӧ�ã��漰����ϵ���������ε����ʡ�ƽ���߷��߶γɱ��������κ��������ʡ�����˼�뼰����˼���֪ʶ���ڣ�1������k��ʾ���ı���OFBE������ǽ���Ĺؼ����ڣ�2��������ƽ���߷��߶γɱ������AB��OA�ij��ǽ���Ĺؼ����ڣ�3������k��ʾ����EFA������ǽ���Ĺؼ������⿼��֪ʶ��϶࣬�ۺ��Խ�ǿ���Ѷ����У�


 �߽�������ϵ�д�
�߽�������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ����ijС��ʵʩ��ů���칤�̣��ּס��������̶ӷֱ�ͬʱ��������600�׳��Ĺܵ������ڹܵ�����y���ף����ھ�ʱ��x���죩֮��Ĺ�ϵ��ͼ��ʾ��������˵���У���ȷ�ĸ����У�����������
����ijС��ʵʩ��ů���칤�̣��ּס��������̶ӷֱ�ͬʱ��������600�׳��Ĺܵ������ڹܵ�����y���ף����ھ�ʱ��x���죩֮��Ĺ�ϵ��ͼ��ʾ��������˵���У���ȷ�ĸ����У�����������| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
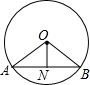 ��ͼ����O�İ뾶Ϊ13����AB�ij�����24��ON��AB������ΪN����ON���ڣ�������
��ͼ����O�İ뾶Ϊ13����AB�ij�����24��ON��AB������ΪN����ON���ڣ�������| A�� | 11 | B�� | 9 | C�� | 7 | D�� | 5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -$\sqrt{3}$ | B�� | $\sqrt{3}$ | C�� | -$\frac{\sqrt{3}}{3}$ | D�� | $\frac{\sqrt{3}}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2017}$ | B�� | 2017 | C�� | -2017 | D�� | -$\frac{1}{2017}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ij��4�·��������ͳ����ͼ��ʾ����������������������У���������λ���ֱ��ǣ�������
ij��4�·��������ͳ����ͼ��ʾ����������������������У���������λ���ֱ��ǣ�������| A�� | 21��21 | B�� | 21��21.5 | C�� | 21��22 | D�� | 22��22 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com