
【题目】已知线段![]() ,点M是线段
,点M是线段![]() 上一动点,以
上一动点,以![]() 为直径作
为直径作![]() ,点C是圆周上一点且
,点C是圆周上一点且![]() ,连接
,连接![]() ,过点A做直线
,过点A做直线![]() 的垂线,交
的垂线,交![]() 于点N,连接
于点N,连接![]() ,设线段
,设线段![]() 的长为
的长为![]() ,线段
,线段![]() 的长为
的长为![]() ,线段
,线段![]() 的长为
的长为![]() .
.

小华同学根据学习函数的经验,分别对函数![]() ,随自变量x的变化而变化的规律进行了探究.
,随自变量x的变化而变化的规律进行了探究.
下面是该同学的探究过程,请补充完整:
(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了![]() 与x的几组对应值:
与x的几组对应值:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 4.47 | 5.24 | 5.86 | 5.96 | 4.72 | 4.00 | |
| 6.00 | 5.86 | 5.23 | 3.98 | 2.46 | 1.06 | 0 |
请你补全表格的相关数值,保留两位小数.
(2)在同一平面直角坐标系![]() 中,描出补全后的表中各组数值所对应的点
中,描出补全后的表中各组数值所对应的点![]() ,
,![]() ,并画出函数
,并画出函数![]() 的图象(函数
的图象(函数![]() 的图象如图,请你画出
的图象如图,请你画出![]() 的图象)
的图象)
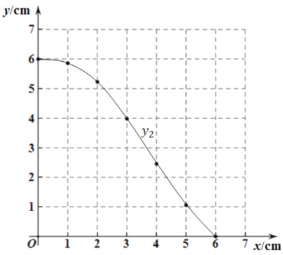
(3)结合画出的函数图象,解决问题:当![]() 是等腰三角形时,
是等腰三角形时,![]() 的长度约为______
的长度约为______![]() .
.
科目:初中数学 来源: 题型:
【题目】近几年购物的支付方式日益增多,某数学兴趣小组就此进行了抽样调查.调查结果显示,支付方式有:A微信、B支付宝、C现金、D其他,该小组对某超市一天内购买者的支付方式进行调查统计,得到如下两幅不完整的统计图.

请你根据统计图提供的信息,解答下列问题:
(1)本次一共调查了多少名购买者?
(2)请补全条形统计图;在扇形统计图中A种支付方式所对应的圆心角为 度.
(3)若该超市这一周内有1600名购买者,请你估计使用A和B两种支付方式的购买者共有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新学期,某校开设了“防疫宣传”“心理疏导”等课程.为了解学生对新开设课程的掌握情况,从八年级学生中随机抽取了部分学生进行了一次综合测试.测试结果分为四个等级:A级为优秀,B级为良好,C级为及格,D级为不及格.将测试结果绘制了如图两幅不完整的统计图.根据统计图中的信息解答下列问题:
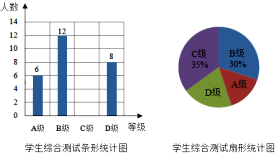
(1)本次抽样测试的学生人数是________名;
(2)扇形统计图中表示A级的扇形圆心角α的度数是________,并把条形统计图补充完整;
(3)该校八年级共有学生500名,如果全部参加这次测试,估计优秀的人数为____;
(4)某班有4名优秀的同学(分别记为E,F,G,H,其中E为小明),班主任要从中随机选择两名同学进行经验分享.利用列表法或画树状图法,求小明被选中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是“作一个![]() 角”的尺规作图过程.
角”的尺规作图过程.
已知:平面内一点A. 求作: |
作法:如图,
①作射线 ②在射线 ③分别以 ④作射线 则 |
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:![]() ,
,
![]() ______
______![]() _______
_______![]() .
.
![]() _____
_____![]() .(_____________)(填推理的依据)
.(_____________)(填推理的依据)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图显示了用计算机模拟随机抛掷一枚硬币的某次实验的结果
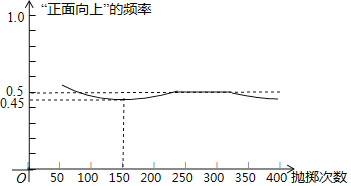
下面有三个推断:
①当抛掷次数是100时,计算机记录“正面向上”的次数是47,所以“正面向上”的概率是0.47;
②随着试验次数的增加,“正面向上”的频率总在0.5附近摆动,显示出一定的稳定性,可以估计“正面向上”的概率是0.5;
③若再次用计算机模拟此实验,则当抛掷次数为150时,“正面向上”的频率一定是0.45.
其中合理的是( )
A.①B.②C.①②D.①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() .将该抛物线在
.将该抛物线在![]() 轴和
轴和![]() 轴下方的部分记作
轴下方的部分记作![]() ,将
,将![]() 沿
沿![]() 轴翻折记作
轴翻折记作![]() ,
,![]() 和
和![]() 构成的图形记作
构成的图形记作![]() .关于图形
.关于图形![]() ,给出如下四个结论,其中错误的是( )
,给出如下四个结论,其中错误的是( )
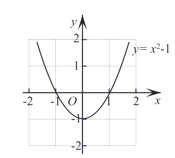
A.图形![]() 恰好经过4个整点(即横、纵坐标均为整数的点)
恰好经过4个整点(即横、纵坐标均为整数的点)
B.图形![]() 上任意一点到原点的距离都不超过1
上任意一点到原点的距离都不超过1
C.图形![]() 的周长大于
的周长大于![]()
D.图形![]() 所围成的区域的面积大于2且小于
所围成的区域的面积大于2且小于![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】过直线外一点且与这条直线相切的圆称为这个点和这条直线的点线圆.特别地,半径最小的点线圆称为这个点和这条直线的最小点线圆.
在平面直角坐标系![]() 中,点
中,点![]() .
.
(1)已知点![]() ,
,![]() ,
,![]() ,分别以
,分别以![]() ,
,![]() 为圆心,1为半径作
为圆心,1为半径作![]() ,
,![]() ,以
,以![]() 为圆心,2为半径作
为圆心,2为半径作![]() ,其中是点
,其中是点![]() 和
和![]() 轴的点线圆的是________;
轴的点线圆的是________;
(2)记点![]() 和
和![]() 轴的点线圆为
轴的点线圆为![]() ,如果
,如果![]() 与直线
与直线![]() 没有公共点,求
没有公共点,求![]() 的半径
的半径![]() 的取值范围;
的取值范围;
(3)直接写岀点![]() 和直线
和直线![]() 的最小点线圆的圆心的横坐标
的最小点线圆的圆心的横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O的直径CD=4,AB是⊙O的弦,AB⊥CD,垂足为M,且AB=2![]() ,则∠ACD等于( )
,则∠ACD等于( )
A.30°B.60°C.30°或60°D.45°或60°
查看答案和解析>>
科目:初中数学 来源: 题型:
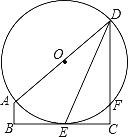
【题目】如图,在直角梯形ABCD中,AB∥CD,∠C=90°,以AD为直径的⊙O与BC相切于点E,交CD于点F,连接DE.
(1)证明:DE平分∠ADC;
(2)已知AD=4,设CD的长为x(2<x<4).
①当x=2.5时,求弦DE的长度;
②当x为何值时,DFFC的值最大?最大值是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com